Содержание
Предисловие профессора С.П. Кулика............................................................................ 13
ЧАСТЬ I.
ОСНОВЫ КВАНТОВОЙ ИНФОРМАТИКИ
Введение..................................................................................................................... 17
ГЛАВА 1.
КВАНТОВАЯ МЕХАНИКА И РАЗВИТИЕ
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ................................................................... 31
1.1.
Менделеев, рождение квантовой механики и оценка
требований к квантовым компьютерам................................................................. 31
1.2.
Закон Мура и развитие информационных технологий........................................ 38
1.3.
Блеск и нищета современной физики................................................................... 40
1.4.
Алгоритм Шора и некоторые другие квантовые алгоритмы................................ 41
1.5.
Кубит vs бит (логический анализ).......................................................................... 44
1.6.
Представление состояния кубита на сфере Блоха................................................ 47
1.7.
Квантовое измерение и квантовый скачок........................................................... 49
1.8.
Системы кубитов и квантовая запутанность......................................................... 50
1.9.
Общие требования, необходимые для реализации квантовых компьютеров...... 54
Выводы к главе 1............................................................................................................... 56
ГЛАВА 2.
ТРИ КИТА, НА КОТОРЫХ ДЕРЖИТСЯ МИР КВАНТОВЫХ ЯВЛЕНИЙ................ 58
2.1.
Объективная случайность...................................................................................... 59
2.2.
Принцип дополнительности.................................................................................. 63
2.3.
Квантовая запутанность, разложение Шмидта и
формализм матрицы плотности............................................................................. 66
Выводы к главе 2............................................................................................................... 70
ГЛАВА 3.
ВЗАИМНО-ДОПОЛНИТЕЛЬНЫЕ КООРДИНАТНОЕ И
ИМПУЛЬСНОЕ ПРЕДСТАВЛЕНИЯ В КВАНТОВОЙ МЕХАНИКЕ......................... 71
3.1.
Статистическая интерпретация прямого и обратного преобразований
Фурье. Координатное и импульсное распределения............................................ 71
3.2.
Принцип дополнительности Н. Бора по отношению
к координатному и импульсному распределениям............................................... 73
3.3.
Характеристическая функция. Вычисление среднего и моментов.
Неполнота классической и полнота квантовой статистики................................. 75
3.4.
Операторы координаты и импульса в координатном и импульсном
представлении. Фундаментальные коммутационные соотношения................... 78
3.5.
Взаимно-дополнительные распределения в опыте Юнга.................................... 79
Выводы к главе 3............................................................................................................... 81
Приложение. Дельта-функция и её свойства.................................................................... 82
ГЛАВА 4.
ТОЧНОСТЬ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК
В КВАНТОВОЙ ИНФОРМАТИКЕ............................................................................ 84
4.1.
Неравенство Коши – Буняковского для векторов состояния и его
статистическая интерпретация.............................................................................. 84
4.2.
Неравенство Коши – Буняковского в приложении
к случайным величинам......................................................................................... 86
4.3.
Соотношение неопределённостей Гейзенберга для координаты и импульса...... 87
4.4.
Соотношение неопредёленностей Шрёдингера – Робертсона............................. 89
Содержание 9
4.5.
Многомерное соотношение неопределённостей.................................................. 91
4.6.
Информация Фишера............................................................................................ 93
4.7.
Неравенство Рао – Крамера................................................................................... 93
4.8.
Многомерное неравенство Рао – Крамера и корневая оценка............................. 96
Выводы к главе 4............................................................................................................... 98
ГЛАВА 5.
ПРИНЦИПЫ КВАНТОВОЙ ИНФОРМАТИКИ И
ШЕСТАЯ ПРОБЛЕМА ГИЛЬБЕРТА......................................................................... 99
5.1.
Постулаты квантовой информатики..................................................................... 99
5.2.
Шестая проблема Гильберта................................................................................. 106
5.3.
Обсуждение........................................................................................................... 108
Выводы к главе 5............................................................................................................. 109
ГЛАВА 6.
КВАНТОВАЯ ИНФОРМАТИКА И КВАНТОВАЯ ФИЗИКА..................................... 111
6.1.
Корневой подход к исследованию механических систем................................... 112
6.2.
Иллюстрация квазиквантового метода моделирования..................................... 117
Выводы к главе 6............................................................................................................. 119
ГЛАВА 7.
ОСНОВНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ КВАНТОВОЙ
ИНФОРМАТИКИ И ИХ СВОЙСТВА...................................................................... 121
7.1.
Квантовые биты.................................................................................................... 121
7.2.
Реализация произвольного состояния кубита посредством
унитарного поворота............................................................................................ 126
7.3.
Система кубитов................................................................................................... 127
7.4.
Измерение кубитов............................................................................................... 128
7.5.
Простейшие квантовые логические элементы.................................................... 129
7.6.
Преобразование Уолша – Адамара....................................................................... 132
7.7.
Теорема о невозможности клонирования неизвестного
квантового состояния........................................................................................... 132
7.8.
Состояния Белла.................................................................................................. 134
7.9.
Парадокс (эффект) Эйнштейна – Подольского – Розена................................... 135
Выводы к главе 7............................................................................................................. 136
ГЛАВА 8.
НЕРАВЕНСТВО БЕЛЛА И МЕХАНИСТИЧЕСКИЙ РЕАЛИЗМ.............................. 137
8.1.
О статистической природе неравенств Белла..................................................... 137
8.2.
Неравенство Белла как мнимый парадокс между
статистикой и квантовой механикой................................................................... 141
8.3.
Восстановление гипотетического совместного распределения
в задаче Белла: подход с использованием разложения
по сингулярным значениям................................................................................. 143
8.4.
Связь между квазивероятностями и формализмом матрицы плотности:
томографическое описание квантовых состояний............................................. 149
8.5.
Задача о существовании гипотетического совместного
распределения для несовместимых наблюдаемых
без использования неравенств. Модель Кошена – Шпеккера........................... 153
8.6.
Трёхкубитовые квантовые состояния Гринбергера – Хорна – Цайлингера....... 156
Выводы к главе 8............................................................................................................. 159
ГЛАВА 9.
НЕКОТОРЫЕ АЛГОРИТМЫ КВАНТОВОЙ ИНФОРМАТИКИ............................. 161
9.1.
Сверхплотное кодирование................................................................................. 161
10
Введение в квантовые информационные технологии
9.2.
Телепортация........................................................................................................ 163
9.3.
Квантовый параллелизм. Алгоритмы Дойча и Дойча – Джозсы........................ 165
9.4.
Квантовое преобразование Фурье....................................................................... 171
9.5.
Нахождение периода функции............................................................................ 174
9.6.
Факторизация чисел............................................................................................. 177
9.7.
Квантовая криптография..................................................................................... 180
9.8.
Алгоритм Гровера................................................................................................. 183
9.9.
Введение в квантовое исправление ошибок....................................................... 186
Выводы к главе 9............................................................................................................. 189
ГЛАВА 10.
НЕКОТОРЫЕ ФИЗИЧЕСКИЕ РЕАЛИЗАЦИИ КУБИТОВ..................................... 190
10.1.
Кубит на спиновом магнитном резонансе.......................................................... 191
10.2.
Поляризационный кубит..................................................................................... 196
10.2.1.
Спиральность электромагнитного поля............................................................. 196
10.2.2.
Когерентное состояние электромагнитного поля в резонаторе........................ 198
10.2.3.
Поляризационное преобразование, задаваемое оптической
фазовой пластинкой............................................................................................ 202
10.3.
Квантовые компьютеры на основе ионов в ловушках........................................ 203
10.3.1.
Ионы в ловушках................................................................................................. 204
10.3.2.
Взаимодействие иона в ловушке с электромагнитным полем.......................... 205
10.4.
Сверхпроводниковый кубит................................................................................ 211
10.4.1.
Эффект Джозефсона. Уравнения для джозефсоновского перехода.................. 211
10.4.2.
Джозефсоновский переход под токовым смещением (управлением).
Уравнение маятника............................................................................................ 213
10.4.3.
Квантование квазимеханической системы........................................................ 215
10.4.4.
Фазовый кубит..................................................................................................... 216
10.4.5.
Измерение фазового кубита................................................................................ 218
10.4.6.
Взаимодействие кубитов..................................................................................... 219
10.5.
Кубиты на основе квантовых точек..................................................................... 219
10.5.1.
Квантовые точки в резонаторе............................................................................ 219
10.5.2.
Теория Флоке (квантовая точка в резонаторе на лазерных качелях)................ 222
10.5.3.
Квантовые преобразования................................................................................ 224
10.6.
Квантовый компьютер на NV-центрах в алмазе................................................. 227
Приложение. Описание поляризационных преобразований
в квантовой физике и классической поляризационной оптике................................... 228
Выводы к главе 10........................................................................................................... 230
ЧАСТЬ II.
АНАЛИЗ КЛАССИЧЕСКИХ И КВАНТОВЫХ СИСТЕМ
ГЛАВА 11.
КОРНЕВАЯ ОЦЕНКА ПЛОТНОСТИ.......................................................................233
11.1.
Метод максимального правдоподобия и информационная
матрица Фишера................................................................................................... 234
11.2.
Корневой подход к оцениванию плотности. Пси-функция и
уравнение правдоподобия.................................................................................... 237
11.3.
Статистические свойства корневых оценок........................................................ 239
11.4.
Некоторые наборы базисных состояний............................................................. 241
11.5.
Набор плотностей распределений, обобщающий гауссово распределение....... 244
11.6.
Аппроксимация распределений с тяжёлыми хвостами.
Волновая функция, приводящая к распределениям
Пирсона IV типа и базисный набор на её основе................................................ 255
Выводы к главе 11........................................................................................................... 264
11
ГЛАВА 12.
УНИФИЦИРОВАННЫЙ МЕТОД КВАНТОВОЙ ТОМОГРАФИИ,
ОСНОВАННЫЙ НА ПРОЦЕДУРЕ ОЧИЩЕНИЯ.................................................. 267
12.1.
Процедура очищения и алгоритм статистического
восстановления квантовых состояний................................................................ 268
12.2.
Точность восстановления квантовых состояний................................................ 272
12.3.
Примеры численного статистического моделирования..................................... 282
Выводы к главе 12........................................................................................................... 284
ГЛАВА 13.
КВАНТОВЫЕ ШУМЫ И КАЧЕСТВО КВАНТОВЫХ ОПЕРАЦИЙ......................... 285
13.1.
Квантовые операции и квантовые шумы............................................................ 287
13.2.
Амплитудная и фазовая релаксация состояний кубитов.................................... 296
13.3.
Математическое моделирование квантовых операций...................................... 302
13.4.
Динамика запутанности в квантовых операциях................................................ 312
Выводы к главе 13........................................................................................................... 318
ГЛАВА 14.
ТОМОГРАФИЯ ОПТИЧЕСКИХ КВАНТОВЫХ СОСТОЯНИЙ............................... 319
14.1.
Основные принципы томографии оптических квантовых состояний.............. 319
14.2.
Базисный набор функций и примеры его использования.................................. 322
14.3.
Реконструкция квантового состояния и информация, содержащаяся
в квантовых измерениях....................................................................................... 327
14.4.
Критерий адекватности томографического эксперимента................................ 329
Выводы к главе 14........................................................................................................... 330
Приложение. Описание поляризационных преобразований
в квантовой физике и классической поляризационной оптике................................... 331
ГЛАВА 15.
СТАТИСТИЧЕСКОЕ ВОССТАНОВЛЕНИЕ ОПТИЧЕСКИХ КВАНТОВЫХ
СОСТОЯНИЙ НА ОСНОВЕ ВЗАИМНО-ДОПОЛНИТЕЛЬНЫХ
КВАДРАТУРНЫХ КВАНТОВЫХ ИЗМЕРЕНИЙ..................................................... 345
15.1.
Измерение квадратурной наблюдаемой.............................................................. 346
15.2.
Статистическое восстановление квантовых состояний..................................... 348
15.3.
Примеры численных экспериментов.................................................................. 351
Выводы к главе 15........................................................................................................... 355
Приложение. Дробное преобразование Фурье............................................................... 355
ГЛАВА 16.
ИССЛЕДОВАНИЕ СТАТИСТИКИ ФОТОНОВ
С ИСПОЛЬЗОВАНИЕМ КОМПАУНД-РАСПРЕДЕЛЕНИЯ
ПУАССОНА И КВАДРАТУРНЫХ ИЗМЕРЕНИЙ.................................................... 359
16.1.
Введение............................................................................................................... 359
16.2.
Производящие функции, статистика фотонов и корреляции............................ 361
16.3.
Условные распределения, отвечающие вычитанию (отщеплению)
фотонов................................................................................................................. 366
16.4.
Квадратурные распределения.............................................................................. 369
16.5.
Делитель пучка: перевод одномерного распределения
в двумерное распределение, корреляция каналов.............................................. 375
16.6.
Многоуровневая иерархия компаунд- распределений Пуассона....................... 377
16.7.
Сжатый вакуум: производящие и корреляционные функции........................... 380
16.8.
Некоторые дополнительные свойства производящих функций и
распределений...................................................................................................... 381
Выводы к главе 16........................................................................................................... 383
Содержание
12
Введение в квантовые информационные технологии
ГЛАВА 17.
ТОМОГРАФИЧЕСКИЙ МЕТОД МОДЕЛИРОВАНИЯ
КВАНТОВЫХ СИСТЕМ.......................................................................................... 384
17.1.
Описание метода.................................................................................................. 386
17.2.
Примеры применения метода.............................................................................. 390
Выводы к главе 17........................................................................................................... 396
Приложение. Диффузионный метод Монте-Карло моделирования
квантовых систем............................................................................................................ 397
ГЛАВА 18.
ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ
МЕТОДАМИ КВАНТОВОЙ ТЕОРИИ..................................................................... 401
18.1.
Представление классических динамических систем на языке
квантовых статистических ансамблей................................................................. 402
18.2.
Описание на основе формализма Гамильтона – Якоби...................................... 405
18.3.
Показатели Ляпунова для систем Лоренца и Рёсслера....................................... 410
Выводы к главе 18........................................................................................................... 413
ГЛАВА 19.
РАЗЛОЖЕНИЕ ШМИДТА И АНАЛИЗ СТАТИСТИЧЕСКИХ
РАСПРЕДЕЛЕНИЙ................................................................................................. 415
19.1.
SVD-разложение и моды Шмидта...................................................................... 415
19.2.
Гауссовы корреляции. Коэффициент корреляции Шмидта.............................. 416
19.3.
Термодинамическая интерпретация................................................................... 418
19.4.
Сравнение результатов аналитических и численных расчётов......................... 420
19.5.
Число Шмидта и коэффициент корреляции..................................................... 421
Выводы к главе 19.......................................................................................................... 424
Приложение 1. Физическая реализация запутанных состояний
посредством двух связанных гармонических осцилляторов........................................ 424
Приложение 2. Вывод формулы для разложения Шмидта
в модели гауссовых корреляций.................................................................................... 425
Приложение 3. Вывод формулы для энтропии запутанности
в модели гауссовых корреляций.................................................................................... 426
ГЛАВА 20.
ИНФОРМАЦИОННЫЕ АСПЕКТЫ ИНТЕРФЕРЕНЦИОННЫХ
ЭКСПЕРИМЕНТОВ «КОТОРЫЙ ПУТЬ» С МИКРОЧАСТИЦАМИ....................... 428
20.1.
Расширение квантовой системы путём добавления новой
переменной. Запутанность с окружением как средство ограничения
квантовой суперпозиции..................................................................................... 431
20.2.
Моды Шмидта...................................................................................................... 434
20.3.
Дифракция на экране с произвольным числом щелей....................................... 436
20.4.
Информационные аспекты задачи дифракции.................................................. 437
20.5.
Моделирование потери когерентности посредством запутанности
со вспомогательной квантовой системой (анциллой)........................................ 439
20.6.
Видность интерференционной картины и когерентность
состояний окружения........................................................................................... 442
20.7.
Реализация запутывания между различными степенями свободы.................... 443
20.7.1.
Поляроиды в щелях............................................................................................. 443
20.7.2.
Использование частотно-координатного запутывания.................................... 444
20.7.3.
Ридберговские атомы в резонаторах................................................................... 444
Выводы к главе 20........................................................................................................... 451
ЛИТЕРАТУРА.......................................................................................................... 452
Предисловие профессора С.П. Кулика
С 90-х годов прошлого века активно развиваются квантовые информаци-
онные технологии, мотивируемые перспективой создания вычислительных
устройств принципиально нового типа с характеристиками, которые недо-
ступны классическим аналогам. В настоящее время в таких устройствах –
квантовых компьютерах и симуляторах – уже продемонстрированы примеры
их превосходства перед классическими компьютерами и появились первые
коммерческие образцы квантовых вычислителей, но пока что с довольно
ограниченными возможностями.
В представляемой читателям книге, рассчитанной на научных работ-
ников, а также аспирантов и студентов, наряду с традиционными методами
квантовой информатики рассматривается и ряд новых подходов, основан-
ных на оригинальных методах и разработках авторов. На мой взгляд, мето-
ды, представленные в книге, весьма интересны и полезны как с фундамен-
тальной, так и с практической точек зрения. Этому во многом способствует
её структура. В первой части представлены общие сведения, составляющие
основу квантовой механики и теории информации, обычно читаемые в соот-
ветствующих разделах университетских курсов физики. Несомненный фун-
даментальный интерес представляет предложенный авторами во второй части
книги симбиоз квантовых и статистических закономерностей, рассматривае-
мый в рамках так называемой шестой проблемы Гильберта, связанной с акси-
оматизацией теории вероятностей. В изложении авторов основой для такой
аксиоматизации, по существу, является математическая модель квантовой те-
ории. Авторы обосновывают, что квантовое состояние можно рассматривать
как естественное обобщение понятия статистического распределения. Важ-
но, что квантовое состояние не может быть сведено к одному-единственному
статистическому распределению, а описывает одновременно совокупность
различных взаимно-дополнительных распределений. Квантовые измерения
таких взаимно-дополнительных распределений лежат в основе методов то-
мографии квантовых состояний и процессов, подробно рассматриваемых
в книге.
Согласно меткому афоризму Людвига Больцмана, «нет ничего практич-
нее, чем хорошая теория». Это целиком относится и к содержанию настоя-
щей книги. Основываясь на глубоком развитии теории, авторы, являющи-
еся сотрудниками Физико-технологического института им. К.А. Валиева
РАН, активно осуществляют разработку методов анализа квантовых систем
и управления ими в задачах контроля качества, стабильности и надежности
систем обработки квантовой информации. Разрабатываемые ими кванто-
вые информационные технологии нацелены на решение проблем, связан-
ных с квантовыми шумами и потерей когерентности квантовых состояний.
14 Введение в квантовые информационные технологии
В основе разрабатываемых авторами подходов лежит оригинальная идея,
связанная с анализом полноты, адекватности и точности реализации кван-
товых вентилей. В своих работах авторы показывают, что математическое
моделирование на базе компьютеров с учётом результатов технологических
и экспериментальных исследований позволяет дать исчерпывающую оценку
качества и эффективности проектируемых и создаваемых систем квантовой
обработки информации, а также сформулировать требования к эксперимен-
тальному оборудованию и технологии. Обращаю внимание, что излагаемые
в книге методы и подходы широко используются в проводимых в настоящее
время экспериментах по построению квантовых вычислительных устройств и
проверке основ квантовой теории. На мой взгляд, эта книга будет интересна
не только физикам, но и математикам, а также представителям других специ-
альностей, активно интересующимся развитием передовых научных направ-
лений и технологий.
Научный руководитель Центра квантовых технологий
физического факультета МГУ,
доктор физико-математических наук, профессор С.П. Кулик
ЧАСТЬ I.
ОСНОВЫ КВАНТОВОЙ
ИНФОРМАТИКИ
ВВЕДЕНИЕ
Век живи – век учись! И ты наконец достигнешь того, что,
подобно мудрецу, будешь иметь право сказать,
что ничего не знаешь.
Козьма Прутков
Инженерные приложения, возникшие на основе квантовой механики, при-
вели во второй половине XX века к технологической революции, которую
сейчас принято называть первой квантовой революцией. Эта технологиче-
ская революция привела к рождению ядерных технологий, а также созданию
транзисторов, лазеров, компьютеров, мобильной связи, Интернета и многого
другого, без чего невозможно представить нашу сегодняшнюю жизнь. Апоге-
ем этой революции, на наш взгляд, стало присуждение Нобелевской премии
по физике в 2000 году за создание основ современных IT-технологий россий-
скому физику Ж. И. Алфёрову совместно с немецким физиком Г. Крёмером и
американским учёным Д. Килби.
Сейчас мир стоит на пороге второй квантовой революции. Её ключе-
вое отличие от первой квантовой революции состоит в том, что если рань-
ше квантовая механика применялась только на уровне «железа» (hardware),
то теперь, в эпоху второй квантовой революции, она оказывается в самой
сердцевине компьютерной логики и программного обеспечения (software).
Логика вычислительных устройств нового типа (квантовых компьютеров) ба-
зируется на применении фундаментальных принципов квантовой механики,
таких как суперпозиция и запутанность квантовых состояний. Компьютеры,
построенные на квантовых принципах, окажутся гораздо эффективнее своих
классических собратьев в решении ряда практически важных классов задач
в области физики, химии, материаловедения, фармацевтики, оптимальных
методов управления, криптографии и др.
Квантовый компьютер представляет собой грандиозный проект, прак-
тическая выгода от которого для общества возможна только в долгосрочной
перспективе [1]. Однако уже сейчас данное направление исследований при-
знаётся обществом очень важным, о чём говорит присуждение Нобелевских
премий по физике в 2012 и 2022 гг. В 2012 году Нобелевская премия по физике
была присуждена французскому физику Сержу Арошу и американскому фи-
зику Дэвиду Вайнленду «за новаторские экспериментальные методы, позволя-
ющие измерять и управлять отдельными квантовыми системами». В 2022 году
Нобелевской премии по физике были удостоены Ален Аспе (Франция),
18 Введение в квантовые информационные технологии
Джон Ф. Клаузер (США) и Антон Цайлингер (Австрия) «за эксперименты
с запутанными фотонами, доказывающие нарушение неравенств Белла и пи-
онерские исследования в квантовой информатике».
Правительства многих стран, в том числе России, финансируют развитие
квантовой отрасли в рамках специальных дорожных карт по квантовым тех-
нологиям. Лидерами по государственной поддержке квантовой отрасли явля-
ются Китай, Европейский союз и США.
В 2019 году правительством РФ на госкорпорацию «Росатом» была возло-
жена ответственность за реализацию дорожной карты, направленной на раз-
витие высокотехнологичной области «Квантовые вычисления». Аналогичная
ответственность за развитие высокотехнологичной области «Квантовые ком-
муникации» была возложена на ОАО «РЖД».
Перспективность квантовых компьютеров обусловлена тем, что некото-
рые вычислительные задачи могут выполняться экспоненциально быстрее
на квантовом процессоре по сравнению с любым современным или перспек-
тивным классическим суперкомпьютером [2]. Следует отметить, что класс
задач, допускающих квантовое ускорение, весьма узок по сравнению с клас-
сом произвольных математических задач [3]. Фундаментальная проблема
заключается в создании высокопроизводительного процессора, способного
выполнять квантовые алгоритмы в экспоненциально большом вычислитель-
ном пространстве. В настоящее время предложены многие десятки различ-
ных физических платформ, на которых могут быть реализованы квантовые
вычисления. Среди наиболее перспективных платформ можно выделить
в том числе системы на основе ионов в ловушках [4–8], системы на основе
атомов в ловушках [9; 10], сверхпроводниковые процессоры [11–13] и фотон-
ные чипы [12].
В 2021 году исследователи из Университета Инсбрука представили де-
монстрационный образец для квантовых вычислений [5], который умеща-
ется в двух 19-дюймовых серверных стойках и представляет собой первый
в мире компактный квантовый компьютер с захваченными ионами, отвечаю-
щий высоким стандартам качества [5].
В январе 2019 года IBM представила новую систему IBM Q System One,
которая является первым коммерческим квантовым компьютером с 20 куби-
тами [11].
Осенью 2019 года группа учёных под руководством Джона Мартини-
са (J. Martinis) из компании Google заявила о достижении так называемо-
го квантового превосходства (quantum supremacy), которое было получено
с использованием квантового процессора Sycamore, состоящего из 53 кубит.
В статье [12], опубликованной в Nature в октябре 2019 года, утверждалось,
что процессор Sycamore выполнил за 200 секунд задание, на которое само-
му мощному на тот момент классическому суперкомпьютеру Summit потре-
бовалось бы 10 тысяч лет. Однако одновременно с публикацией результатов
Google специалисты компании IBM выступили с попыткой их опровержеВведение
19
ния, утверждая, что в такой вычислительной классической системе, как
Summit, рассматриваемая задача может быть решена всего 2,5 дня или даже
быстрее [14].
В декабре 2020 года группа китайских учёных из the University of Science
and Technology of China (USTC) с целью продемонстрировать квантовое пре-
восходство реализовала бозонные выборки на 76 фотонах с помощью фотон-
ного квантового компьютера Jiuzhang [15]. Авторы утверждают, что класси-
ческому современному суперкомпьютеру потребуется 600 миллионов лет
вычислительного времени, чтобы сгенерировать количество отсчётов, кото-
рое их квантовый процессор может сгенерировать за 20 секунд.
Несмотря на интенсивное развитие квантового компьютинга в течение
более тридцати лет, создание полномасштабного квантового компьютера всё
ещё остаётся недостижимой мечтой для современных технологий. Вместе
с тем исследования, выполненные в последние годы, показали, что квантовое
ускорение достижимо в реальной системе и не запрещено никакими скрыты-
ми физическими законами. Можно констатировать, что существенный про-
гресс в области экспериментальных и технологических исследований вселя-
ет реальную надежду на создание в среднесрочной перспективе квантовых
вычислительных устройств, способных решать практически важные задачи.
Достигнутый уровень квантовых информационных разработок провозгла-
шает новую эру NISQ- (Noisy Intermediate Scale Quantum) технологий. Та-
кие технологии сами по себе ещё до создания полномасштабных квантовых
компьютеров открывают новые довольно широкие вычислительные возмож-
ности, которые включают в себя методы оптимизации, машинное обуче-
ние, материаловедение, химию, а также ряд других научных и практических
областей.
Необходимо обеспечить непрерывное совершенствование NISQ-
технологий с тем, чтобы с течением времени открывались бы возможности
для решения всё более сложных задач. Для решения поставленных задач кри-
тически важно разработать систему непрерывного мониторинга и прогнози-
рования характеристик точности и эффективности квантовых информацион-
ных устройств в зависимости от степени их интеграции для вычислительных
задач различной сложности и для различных уровней декогерентизации и
квантовых шумов [16; 17].
Наряду с математическим моделированием квантовых операций и алго-
ритмов необходимо осуществлять их контроль в условиях реального экспери-
мента. Основным инструментом для этих целей служит томография кванто-
вых состояний и процессов [18–24], которая призвана обеспечить интерфейс
между разработкой элементной базы квантовых компьютеров и симуляторов
и её практическим воплощением. Методы численного анализа и статистиче-
ского моделирования с учётом влияния квантовых шумом, а также резуль-
татов технологических и экспериментальных исследований позволяют дать
исчерпывающую оценку качеству и эффективности проектируемых кван-
20 Введение в квантовые информационные технологии
товых регистров, сформулировать требования к экспериментальному обо-
рудованию и технологии; посредством обратной связи развиваемый подход
позволяет наилучшим образом распорядиться имеющимися ресурсами для
оптимизации процесса разработки квантовых информационных технологий.
Заметим, что наряду с томографией активно развиваются методы кван-
тового контроля, направленные на управление динамикой физических про-
цессов на атомном и молекулярном уровнях [25–28]. Это область науки
с многочисленными приложениями, начиная от селективных лазерно-инду-
цированных атомных и молекулярных возбуждений и заканчивая квантовы-
ми вычислениями и управлением химическими реакциями с помощью спе-
циально подобранных лазерных импульсов.
В России наиболее совершенным прототипом квантового процессора на
сегодня (август 2024 г.) является процессор на ионах в ловушках, реализован-
ный в ФИАН на 25 четырехуровневых кудитах (что эквивалентно степени
интеграции в 50 кубитов). Заметим, что кудиты представляют собой перспек-
тивную платформу для масштабируемых квантовых вычислений [29; 30]. Ак-
тивные работы в области элементной базы квантовых информационных тех-
нологий ведутся также в Российском квантовом центре, Центре квантовых
технологий МГУ, в МФТИ, МИСИС и ряде других организаций.
В 2022 году продемонстрирована технология массового производства
спиновых кубитов на кремниевых пластинах диаметром 300 мм с исполь-
зованием ультрафиолетовой 193-нм иммерсионной литографии (Intel) [31].
Эти достижения могут в недалёком будущем вывести кремниевую платформу
в число основных. В России конструкция квантового компьютера на осно-
ве квантовых точек в каналах полевых транзисторов в кремнии была пред-
ложена во ФТИАН им. К.А. Валиева ещё в конце 90-х гг. [32; 33]. В 1998 году
австралийский физик Б. Кейн (B.E. Kane) предложил использовать в каче-
стве кубита ядерный спин одиночного атома фосфора 31P, имплантирован-
ного в бесспиновый кремний 28Si. Очевидно, что это предложение содержит
синтез методов и материалов из магнитного резонанса и микроэлектроники.
В развитие идеи Кейна К.А. Валиев и А.А. Кокин в 1999 году предложили
строить кубит на ансамбле спинов атомов 31P в 28Si, т. е. использовать спины
многих атомов 31P, а не одного атома. Результаты исследований были обобще-
ны в монографии А.А. Кокина [34].
Другая перспективная твердотельная модель – это квантовые компью-
теры на электронных состояниях в квантовых точках в полупроводниковых
структурах. Преимущества этой схемы обусловлены высокой скоростью вы-
полнения логических операций, возможностью измерения состояний от-
дельных кубитов (благодаря более высокой интенсивности сигнала по срав-
нению с отдельными ядерными спинами), более простыми по сравнению
с ЯМР способами управления кубитами, а также тем, что рассматриваемые
устройства могут работать при более высоких температурах, чем твердотель-
ные ЯМР квантовые регистры. Трудности реализации рассматриваемой мо-
Введение 21
дели связаны с жесткими требованиями к технологии изготовления много-
кубитовых регистров, а также малыми временами релаксации электронных
состояний по сравнению с такими же временами для ядерных спинов.
Основой для рассматриваемой модели может служить зарядовый кубит
на сформированной в арсениде галлия квантовой точке, разделенной управ-
ляемым потенциальным барьером с одним электроном [35]. Проведённое
в работе Л.Е. Федичкина, М. Янченко и К.А. Валиева численное моделиро-
вание показало, что в рассматриваемом случае низкие температуры (~ 1 мК)
обеспечивают исходную инициализацию и требуемую когерентность. В каче-
стве логических состояний «ноль» и «единица» могут служить локализован-
ные состояния электрона в минимумах потенциала при достаточно большой
высоте потенциального барьера. Теоретический анализ доказал возможность
реализации в рассматриваемой модели квантовых однокубитовых, а также
двухкубитовых (например CNOT) операций.
В настоящее время исследования полупроводниковых систем кубитов
проводятся во ФТИАН им. К.А. Валиева и в Институте физики микрострук-
тур РАН.
В препринте [36], опубликованном в апреле 2023 большим авторским
коллективом исследователей Google (более 150 человек), говорится о созда-
нии квантового компьютера Google нового поколения, содержащего 70 ку-
битов. Новый процессор является непосредственным развитием процессора
Sycamore, созданного ещё в 2019 году. Утверждается, что новый квантовый
процессор способен за 6,7 секунд выполнить вычисления, на которые у са-
мого мощного на тот момент суперкомпьютера Frontier ушло бы 47 лет. Во-
прос о степени состоятельности претензий Google на достижение квантового
превосходства с помощью процессора Sycamore первого поколения оставался
актуальной темой научных дискуссий в течение нескольких лет [37]. По мне-
нию исследователей, сомнения о том, достиг ли процессор Google квантового
превосходства, теперь, после создания процессора Sycamore второго поколе-
ния, разрешены в пользу Google.
В 2023 году компания IBM выполнила исследование с использованием
«шумного» квантового процессора Eagle (127 кубит). В том же 2023 году груп-
па исследователей из IBM опубликовала в Nature статью, которая, по мне-
нию авторов, убедительно доказывает практическую полезность квантовых
вычислений [38]. Результаты выполненного эксперимента показывают, что
и до того, как будет обеспечена отказоустойчивость (fault tolerance) кван-
товых схем, полезные результаты можно получать на «шумном» квантовом
компьютере. Авторы отмечают, что квантовые вычисления обещают су-
щественно ускорить решение определённых задач по сравнению с их клас-
сическими «собратьями», однако самым большим препятствием на пути
полномасштабной реализации квантовых вычислений является шум, прису-
щий квантовым информационным системам. Стандартным решением этой
проблемы была бы реализация отказоустойчивых квантовых схем, однако
22 Введение в квантовые информационные технологии
это недостижимо для современного уровня технологии. В экспериментах
на шумном 127-кубитном
процессоре Eagle демонстрируется высокоточное
измерение средних значений (математических ожиданий) в задачах, масштаб
которых многократно превосходит возможности классических вычислений
методом «грубой силы». Авторы не используют методы коррекции ошибок
(error correction), требующие колоссального числа вспомогательных кубитов.
Вместо этого они используют методы «смягчения» ошибок (error-mitigation),
основанные на постобработке результатов квантовых измерений.
В рассмотренной авторами задаче, связанной с моделью Изинга, ради-
кальное преимущество квантового процессора по сравнению с классическим
относится к масштабу задачи: ни один классический компьютер не имеет
столько памяти, чтобы можно было бы закодировать результаты, отвечающие
возможностям 127-го регистра кубитов (заметим, что 2127 = 1.7e + 38).
Заметим также, что эксперимент проводился на 127-кубитном процес-
соре Eagle, а не на более новом процессоре компании Osprey с 433 кубита-
ми, представленном ещё в ноябре 2022 года. Основной причиной сделанно-
го IBM выбора в пользу менее масштабного процессора Eagle является то,
что он уже прошёл третью итерацию улучшений (Revision 3), в то время как
Osprey всё ещё находится на первой экспериментальной итерации. Осущест-
влённые на Eagle модификации привели к увеличению производительно-
сти процессора, а также к снижению уровня шума, что облегчило процедуру
error-mitigation. Важно также иметь в виду, что сама процедура error-mitigation
масштабируется экспоненциально с числом кубитов, поэтому имеющихся
в настоящее время суперкомпьютерных мощностей просто недостаточно для
реализации полномасштабной процедуры error-mitigation на квантовом про-
цессоре Osprey.
Заметим, что в январе 2024 г. в журнале PRX QUANTUM группа иссле-
дователей из США сообщила о точном и эффективном классическом моде-
лировании квантовой системы Изинга на решётке тяжёлых шестиугольни-
ков [39]. Моделирование как раз этой системы было выполнено в 2023 году
на 127-кубитном квантовом процессоре Eagle IBM с использованием ме-
тодов смягчения ошибок для повышения точности [38]. Авторы показали,
что, приняв подход тензорной сети, который отражает геометрию решётки,
можно выполнить классическое моделирование, которое значительно более
полное и точное, чем результаты, полученные с помощью квантового про-
цессора. Авторы также показывают, что их метод позволяет выполнять моде-
лирование системы на длительных временах в термодинамическом пределе,
соответствующем квантовому компьютеру с бесконечным числом кубитов.
По мнению авторов, их подход тензорных сетей имеет более широкое приме-
нение для моделирования динамики квантовых систем такого рода. На наш
взгляд, работы, подобные [39], свидетельствуют об активной разработке но-
вых классических методов и алгоритмов, само появление которых мотивиро-
вано развитием квантовых информационных технологий. Такое соперниче-
Введение 23
ство между классическими и квантовыми алгоритмами несёт несомненную
пользу для обеих отраслей.
О перспективных и неперспективных задачах для квантовых компью-
теров с точки зрения достижения квантового преимущества говорится
в статье [40], опубликованной в мае 2023 года в журнале Communication of
the ACM, представляющем ассоциацию вычислительной техники (ACMAssociation
for Computing Machinery). Отметим, что ACM – старейшая и са-
мая крупная международная организация в компьютерной области, которая
объединяет 83 000 специалистов. Авторы статьи (сотрудники Microsoft) ста-
вят своей целью отделение шумихи вокруг квантовых технологий от прак-
тических задач, в которых возможно реальное достижение квантового
преимущества (quantum advantage). По мнению авторов статьи, многие со-
временные квантовые алгоритмы могут так и не достичь практического
ускорения. В то же время материаловедение и химия имеют огромный по-
тенциал и можно надеяться, что будут изобретены практичные квантовые ал-
горитмы. Из-за ограничений входной и выходной пропускной способности
квантовые компьютеры будут практичны для задач big compute – больших
вычислений с небольшим количеством данных, но не для задач с большим
количеством данных – big data. Квадратичное ускорение, обеспечиваемое
такими алгоритмами, как алгоритм поиска Гровера, недостаточно для прак-
тического квантового преимущества без значительных улучшений всего
программно-аппаратного стека.
В рамках квантовых информационных технологий важное значение име-
ет задача целочисленной факторизации. Для решения данной задачи с помо-
щью стандартных квантовых вычислений используется алгоритм Шора [41].
Однако экспериментальная реализация алгоритма Шора в гейтовом кванто-
вом вычислителе – крайне непростая задача. Например, авторы известной
работы [42] использовали молекулу с семью ядрами со спином 1/2 для фак-
торизации числа 15. Но подобные эксперименты не могут быть применены
для факторизации больших чисел, что приводит к необходимости улучшения
данного алгоритма. Так, в работе [43] предлагается использовать реинициа-
лизируемые кубиты для реализации итеративной вариации алгоритма Шора.
Одним из наилучших результатов при использовании данного алгоритма
остаётся разложение чисел 51 и 85 с помощью квантовой схемы на восьми
кубитах [44]. В течение последних десятилетий было предпринято много по-
пыток реализовать гейтовый алгоритм Шора на различных квантовых вы-
числительных устройствах. Однако квантовые вычисления являются техно-
логией, которая только начинает своё развитие, и существующие квантовые
устройства всё ещё имеют ограниченные возможности и неспособны решать
сложные проблемы, такие как факторизация больших чисел, которые явля-
ются основой криптографических алгоритмов.
В настоящее время активно разрабатываются методы атак на криптогра-
фические алгоритмы, альтернативные подходам с использованием алгоритмов
24 Введение в квантовые информационные технологии
Шора и Гровера. Так, в конце 2022 года группой китайских учёных в препринте
[45] был представлен метод факторизации чисел, совмещающий классический
метод Шнорра [46; 47] и квантовый алгоритм QAOA (Quantum Approximate
Optimization Algorithm – квантовый алгоритм приближенной оптимизации).
Авторы работы утверждают, что разложили с использованием реальных кван-
товых вычислителей самое большое на данный момент 15-значное число
N = 261980999226229 = 15538213 ⋅ 16860433, а также делают оценку, что
с использованием предложенного метода RSA-2048 может быть взломан
на 372 физических кубитах. В связи с последним утверждением работа вы-
звала большой новостной резонанс [48; 49]. Однако профессиональное со-
общество отнеслось к данной работе скептически [50] и стали появляться ра-
боты с указанием конкретных [51] проблем в работе [45]. Сами оригинальные
работы Шнорра вызывают множество вопросов, а предложенный метод не
показал успешной работы на реальных задачах, предложенный же гибридный
метод с использованием алгоритма QAOA данных проблем не разрешает.
Отметим, что в методе Шнорра и соответствующем квантовом расши-
рении задача факторизации чисел сводится к минимизации, что и служит
поводом для использования квантовых вычислителей. Описанная работа
не является первой в данном направлении. Так, например, рассматривались
подходы с использованием квантовых адиабатических алгоритмов [52–54] и
вариационных квантовых алгоритмов [55; 56]. Помимо работы [45] есть и ряд
других работ с факторизацией различных чисел с использованием квантовых
вычислителей [57–60]. Так, в препринте [61] утверждается, что на 10 ионных
кубитах при помощи цифровизованного квантового контрадиабатического
алгоритма было разложено 48-битное число. Однако такие работы имеют ряд
типичных проблем: лишь часть расчётов производится при помощи кванто-
вых вычислителей, выбираются специальные удобные для алгоритмов числа,
представляются нереалистичные оценки масштабируемости. Также стоит от-
метить, что сама возможность получения квантового ускорения при помощи
подобных оптимизационных алгоритмов на данный момент остаётся откры-
тым вопросом.
В январе 2024 г. вышел довольно объёмный препринт (75 стр.), посвя-
щённый оценке преимуществ и рисков, связанных с квантовыми компью-
терами [62]. Работа написана сотрудниками IBM, NIST, Microsoft и ряда
других организаций США и Канады, специализирующихся на квантовых вы-
числениях и информационной безопасности. Авторы препринта отмечают,
что квантовые вычисления — это новая технология, имеющая потенциаль-
но далеко идущие последствия для национального процветания и безопас-
ности. Понимание временных рамок, в течение которых могут проявиться
экономические выгоды и риски национальной безопасности (в частности,
посредством криптоанализа), имеет жизненно важное значение для обеспе-
чения разумного развития этой технологии. Чтобы информировать экспер-
тов по безопасности и лиц, принимающих политические решения по этому
Введение 25
вопросу, авторы, используя имеющуюся на сегодня исследовательскую лите-
ратуру, рассматривают то, что в настоящее время известно о потенциальном
использовании и рисках квантовых компьютеров. Отмечается, что степень
зрелости доступных в настоящее время квантовых компьютеров ещё не до-
стигла такого уровня, чтобы их можно было использовать в производстве
для решения крупномасштабных, промышленно важных задач, и в насто-
ящее время считается, что квантовые компьютеры пока что не представля-
ют угрозу безопасности для классических информационных систем. Вместе
с тем можно выделить две крупномасштабные тенденции — разработку но-
вых приближенных методов (вариационные алгоритмы, смягчение ошибок
и объединение схем), а также коммерческие исследования квантовых прило-
жений, важных для бизнеса. Вместе эти две тенденции могут сделать возмож-
ными полезные и практичные квантовые вычисления в ближайшем будущем.
В то же самое время обсуждаемые новые приближенные методы вряд ли из-
менят необходимые ресурсы для криптоанализа, применяемые к используе-
мым в настоящее время криптосистемам. Анализ существующих и известных
алгоритмов криптоанализа показывает, что они требуют схем, размер которых
превышает те, которые могут быть реализованы современными квантовыми
компьютерами или квантовыми вычислителями, которые могут появиться
в обозримом будущем. Важно отметить, однако, что в литературе встречают-
ся улучшенные квантовые алгоритмы для такого рода задач. Кроме того, риск
для кибербезопасности можно эффективно контролировать за счёт перехода
на новые квантовобезопасные (постквантовые) криптографические прото-
колы. Таким образом, достоверно можно ожидать, что квантовые компью-
теры будут способны выполнять экономически выгодные вычисления, пре-
жде чем они станут пригодны для выполнения операций, которые являются
криптографически релевантными.
Среди новостей последнего времени в области квантовых информацион-
ных технологий отметим следующие.
В марте 2024 года Google совместно с XPRIZE и Женевским форумом
науки и дипломатии (Geneva Science and Diplomacy Anticipator – GESDA)
объявила о запуске трёхлетнего международного конкурса XPRIZE с бюдже-
том в 5 млн. долларов по применению квантовых вычислений для решения
прикладных задач [63]. Конкурс направлен на создание алгоритмов кванто-
вых вычислений, которые можно будет применить на практике (сегодня или
в будущем) для достижения общественно полезных целей, подобных тем, ко-
торые описаны в целях устойчивого развития Организации Объединенных
Наций. Инициаторы отмечают, что конкурс тесно связан со стремлением
квантовой команды Google создать крупномасштабный квантовый компью-
тер с исправлением ошибок и разработкой полезных приложений для кван-
товых вычислений. Таким образом, компания Google заявляет о поддержке
применения новых квантовых технологий для решения крупных задач, име-
ющих глобальный характер.
26 Введение в квантовые информационные технологии
Компания IBM анонсировала аппаратное и программное обеспече-
ние эпохи квантовой полезности, а также дорожную карту до 2033 года [64].
По мнению IBM, эксперимент, описанный ими в июне 2023 года в журнале
Nature [38], изменил существовавший до этого статус-кво. В [38] было проде-
монстрировано, что квантовые компьютеры могут управлять схемами, недо-
ступными для классического моделирования методом «грубой силы». Впер-
вые возникло аппаратное и программное обеспечение, способное выполнять
квантовые схемы без известного априорного ответа в масштабе порядка
100 кубитов и 3000 вентилей. Квантовый компьютер теперь, по мнению IBM,
является вычислительным инструментом, что открывает возможность раз-
вивать науку в областях, выходящих за рамки самих квантовых вычислений.
Из таких крупномасштабных экспериментов стало ясно, что нужно выйти
за рамки традиционных моделей квантовых схем и воспользоваться преиму-
ществами параллелизма в условиях параллельных классических вычислений
и квантовых динамических схем. Появляются новые квантовые алгоритмы,
которые используют несколько потенциально параллельных квантовых схем
с одновременными классическими операциями. Становится очевидным,
что требуется гетерогенная вычислительная архитектура, состоящая из мас-
штабируемого и параллельного выполнения квантовых схем и продвинутых
классических вычислений.
Ещё 4 декабря 2023 г. на ежегодном саммите IBM Quantum Summit
в Нью-Йорке компания IBM представила новейший 133-кубитный кванто-
вый процессор Heron («Цапля») и первый модульный квантовый компьютер
IBM Quantum System Two на его базе. IBM также анонсировала процессор
Condor с 1121 кубитом, который имеет на 50% большую плотность кубитов
по сравнению с IBM Osprey. Как считают в IBM, усилия по созданию этого
устройства открыли путь к масштабированию квантовых вычислений. Про-
цессор Condor является частью долгосрочных исследований IBM по разра-
ботке крупномасштабных квантовых вычислительных систем. Хотя он рас-
полагает огромным количеством кубитов, производительность его сравнима
с 433-кубитным устройством Osprey, представленным в 2022 году. Это связано
с тем, что простое увеличение количества кубитов без изменения архитек-
туры не делает процессор быстрее или мощнее. По мнению представителей
IBM, опыт, полученный при разработке Condor и предыдущих процессоров
(127-кубитного Eagle и 433-кубитного Osprey), проложил путь к прорыву
в перестраиваемой архитектуре на базе процессора Heron. IBM рассматрива-
ет Quantum Heron как самый производительный на сегодняшний день кван-
товый процессор IBM с новой архитектурой, обеспечивающей пятикратное
снижение уровня ошибок.
Квантовая команда IBM возлагает большие надежды на отмеченный
выше вычислитель Quantum System Two, первый модульный квантовый ком-
пьютер компании [65]. По мнению компании, новое устройство представля-
ет собой краеугольный камень квантовоцентрической суперкомпьютерной
Введение 27
архитектуры IBM. Первая такая IBM Quantum System Two, расположенная
в Йорктаун-Хайтс в штате Нью-Йорк, уже начала работу с тремя процессо-
рами IBM Heron и вспомогательной управляющей электроникой. На новом
133-кубитном процессоре IBM Quantum Heron уже проводятся эксперимен-
ты, для выполнения которых IBM предоставляет пользователям доступ через
облако. В число таких пользователей входит Аргонская национальная лабо-
ратория Министерства энергетики США, Токийский университет, Вашинг-
тонский университет, Кёльнский университет, Гарвардский университет и
др. Дополнительные процессоры IBM Heron присоединятся к парку систем
общего назначения IBM в течение 2024 года. IBM продлила дорожную кар-
ту развития IBM Quantum до 2033 года и разработала дорожную карту IBM
Quantum Innovation до 2029 года [66].
В области квантового программного обеспечения 9 марта 2024 г. в соот-
ветствии с планами, озвученными ещё в декабре 2023 г., IBM официально вы-
пустила версию программной среды 1.0 Qiskit [67]. Программная среда Qiskit и
связанный с ней генеративный искусственный интеллект упрощают програм-
мирование квантового компьютера. Кроме того, в целях упрощения процесса
разработки квантовых вычислений IBM анонсирует Qiskit Patterns. Это при-
ложение будет служить механизмом, который позволит квантовым разработ-
чикам легче создавать программный код. Оно основано на наборе инструмен-
тов, позволяющих просто отображать классические задачи, оптимизировать
их для квантовых схем с помощью Qiskit, выполнять эти схемы с помощью
Qiskit Runtime и затем обеспечивать постобработку результатов. С помощью
Qiskit Patterns в сочетании с Quantum Serverless пользователи смогут создавать,
развертывать и выполнять рабочие процессы, интегрирующие классические и
квантовые вычисления в различных средах, таких как облачные или локаль-
ные сценарии. Все эти инструменты предоставят пользователям строительные
блоки, которые позволят легче создавать и запускать квантовые алгоритмы.
В феврале 2024 г. в США открылось первое специализированное пред-
приятие для массового выпуска квантовых компьютеров [68]. Двери завода
компании IonQ были открыты в присутствии делегации от властей штата
Вашингтон. Квантовые компьютеры IonQ выглядят как обычные серверные
стойки, и этим они подкупают заказчиков, среди которых ряд крупнейших
компаний из США и других стран, а также Пентагон. В настоящий момент
компания способна производить и поставлять заказчикам квантовые систе-
мы Forte на 35 алгоритмических кубитах, и в будущем компания запустит
сборку систем Tempo на 64 алгоритмических кубитах. Квантовая платформа
IonQ опирается на кубиты из ионов под управлением лазеров. Такие систе-
мы не требуют криогенного охлаждения или, по крайней мере, охлаждаются
до относительно высоких температур. Это делает работу с ними удобной и
достаточно экономичной по затратам. По утверждению IonQ, когда-нибудь
заводы по производству квантовых компьютеров будут открываться десятка-
ми, но первый останется таким навсегда.
28 Введение в квантовые информационные технологии
В статье, опубликованной в Nature в марте 2024 г. [69], исследователи
из California Institute of Technology (США) выполнили бенчмаркинг точно-
сти и оценку запутанности в смешанных состояниях с помощью 60-атом-
ного аналогового квантового симулятора Ридберга. Рассматривался режим
высокой энтропии запутанности, в котором точное классическое моделиро-
вание становится практически невозможным. Рассматриваемый протокол
сравнительного тестирования включал экстраполяцию результатов сравне-
ний с приближенным классическим алгоритмом с различными пределами
запутанности. Авторы разработали и продемонстрировали систему оценки
экспериментальной запутанности в смешанных состояниях, обнаружив, что
предложенная система способна конкурировать с современными цифровы-
ми квантовыми устройствами, выполняющими эволюцию случайных цепей.
Авторы сравнили экспериментальную точность с точностью, достигнутой
различными приближенными классическими алгоритмами, и обнаружили,
что только предлагаемый ими алгоритм способен адекватно описывать экс-
перимент. По мнению авторов, полученные результаты позволяют создать
новую модель для оценки способности аналоговых и цифровых квантовых
устройств генерировать запутанность в сверхклассическом режиме, что под-
чёркивает разрыв между квантовыми и классическими системами.
Одним из новейших направлений развития квантовых информационных
технологий является квантовый интернет, который развивается на основе
симбиоза квантовых вычислений, квантовых коммуникаций и квантовой
сенсорики. Организационно квантовый интернет представляет собой инфор-
мационную систему, которая объединяет совокупность различных квантовых
устройств в единую глобальную сеть. В качестве соответствующих устройств,
входящих в квантовую сеть, могут выступать различные квантовые процессо-
ры, квантовая память и пр. В качестве информационного ресурса квантово-
го интернета выступают квантовые состояния. Принципиально важно уметь
создавать, передавать, преобразовывать и измерять так называемые запутан-
ные квантовые состояния, способные обеспечивать наличие квантовых кор-
реляций между различными разделёнными в пространстве квантовыми под-
системами.
В качестве базовых технологий квантового интернета могут выступать не
только технологии квантового распределения ключей, но и такие техноло-
гии, как распределённые квантовые вычисления, так называемые квантовые
вычисления «вслепую», сенсорные квантовые сети и пр. Так, распределённые
квантовые вычисления, реализуемые в рамках квантового интернета, обе-
спечивают новые недоступные классическим компьютерам вычислительные
возможности, создаваемые посредством связей между удаленными кванто-
выми узлами. Благодаря функциональным возможностям, предоставляемым
квантовым интернетом, удаленные квантовые устройства могут взаимодей-
ствовать и кооперироваться между собой для решения сложных вычисли-
тельных задач, недоступных для распределенных классических вычислений.
Введение 29
Облачные подходы, при которых пользователи могут удаленно полу-
чать доступ к квантовым серверам, уже стали важной технологией, доступ-
ной современным пользователям, которые могут выполнять вычисления
на коммерчески доступных квантовых вычислительных устройствах. Одна-
ко делегирование квантовых вычислений серверу сопряжено с проблемами
конфиденциальности и безопасности, которые точно так же ограничивают
и классические облачные вычисления. В настоящее время пользователи не
могут скрыть свою работу от сервера или самостоятельно проверить свои ре-
зультаты. Однако примечательно, что законы квантовой физики позволяют
создать технологии квантовых вычислений «вслепую». Новые технологии
могут оставить сервер «слепым» таким образом, что скроются входные, вы-
ходные данные и алгоритм клиента. Поскольку квантовая информация не
может быть скопирована, а измерения необратимо изменяют квантовое со-
стояние, информация, хранящаяся в этих системах, может быть защищена
с помощью квантовой теоретико-информационной безопасности. Важно,
что неправильная работа сервера или попытки атаки могут быть обнаружены
(удивительная возможность, которой нет в классических вычислениях).
В апреле 2024 г. группа исследователей Imperial College London опубли-
ковала в журнале Science Advances статью «Детерминированное хранение
и извлечение телекоммуникационного света из однофотонного источни-
ка на квантовых точках, соединенного с атомной квантовой памятью» [70].
Был реализован гибридный интерфейс твердотельных однофотонных ис-
точников и атомной квантовой памяти, что являлось давней целью фотон-
ных квантовых технологий. Авторы продемонстрировали детерминирован-
ное хранение и извлечение света из полупроводниковой квантовой точки
в квантовой памяти атомного ансамбля на телекоммуникационных длинах
волн. Хранились одиночные фотоны из квантовой точки арсенида индия
в широкополосной квантовой памяти на основе паров рубидия с общей эф-
фективностью внутренней памяти (12,9 ± 0,4)%. Отношение сигнал/шум
полученного светового поля составляло 18,2 ± 0,6 и ограничивалось только
темновыми отсчётами детектора. Заметим, что квантовая память представ-
ляет собой квантово-механическую версию обычной компьютерной памяти.
В то время как обычная память хранит информацию в виде двоичных клас-
сических состояний (представленных в виде 0 и 1), квантовая память хранит
целое квантовое состояние для последующего извлечения. Квантовая память
может использоваться в самых разных областях, включая квантовые вычис-
ления и квантовую связь [71–74].
В статье, опубликованной в апреле 2024 г. в журнале Physical Review
Letters [75], исследователи из University of Oxford (Великобритания) сообща-
ют о первой гибридной вещественно-фотонной (matter-photon) реализации
поддающихся проверке слепых квантовых вычислений. Авторы использова-
ли квантовый сервер захваченных ионов и клиентскую систему фотонного
обнаружения, объединенные в сеть через оптоволоконную квантовую связь.
30 Введение в квантовые информационные технологии
Наличие кубитов памяти и детерминированных шлюзов запутанности позво-
лило использовать интерактивные протоколы без постселекции — ключевое
требование для любого масштабируемого слепого сервера, которое ранее не
могло быть обеспечено. Авторы количественно оценили потерю конфиден-
циальности как ≤ 0,03 утечки классических битов на кубит (Fidelity > 97%).
Выполненный эксперимент, по мнению авторов, демонстрирует путь к пол-
ностью доверенным квантовым вычислениям в облаке.
Важными системами, которые могут быть реализованы в рамках кван-
тового интернета, являются системы квантового позиционирования и кван-
тового определения дальности с помощью распределённой сенсорной сети.
Такого рода системы квантового позиционирования и квантового ориенти-
рования могут быть созданы, в частности, с использованием сетевых радаров
с фазированной решёткой и квантовым усилением на основе квантовых со-
стояний многочастной запутанности в непрерывных переменных. Оказыва-
ется, что использование сенсорной сети для квантового позиционирования
и квантового определения дальности обеспечивает существенное преиму-
щество в точности в трёхмерном пространстве по сравнению с классической
схемой, также существенно увеличивая дальность обнаружения объектов.
Настоящая книга включает в себя 20 глав, сгруппированных в две ча-
сти. В первой части изложены основы квантовой информатики, во второй
части рассматривается приложение методов квантовой информатики к ана-
лизу классических и квантовых систем. Материал книги основан на лекциях,
которые в течение ряда лет читались авторами студентам Центра квантовых
технологий физического факультета МГУ, студентам кафедры квантовой фи-
зики и наноэлектроники Национального исследовательского университе-
та электронной техники (НИУ МИЭТ), а также студентам кафедры физики
конденсированных сред Национального исследовательского ядерного уни-
верситета МИФИ (НИЯУ МИФИ).
Авторы благодарны всем своим коллегам и ученикам за научное сотруд-
ничество в области квантовых технологий. Наша особая признательность
Борису Бантышу, Дмитрию Фастовцу, Андрею Чернявскому, Гранту Авосо-
пянцу, Константину Катамадзе и Юрию Кузнецову за помощь в подготовке
настоящего издания.
ГЛАВА 1.
КВАНТОВАЯ МЕХАНИКА И
РАЗВИТИЕ ИНФОРМАЦИОННЫХ
ТЕХНОЛОГИЙ
Где начало того конца, которым оканчивается начало?
Козьма Прутков
Настоящая глава является вводной. В ней представлен обзор квантовых тех-
нологий обработки информации «с высоты птичьего полёта».
1.1. Менделеев, рождение квантовой
механики и оценка требований
к квантовым компьютерам
8 февраля 2024 года исполнилось 190 лет со дня рождения Д.И. Менделеева.
В настоящем разделе в историческом контексте мы развиваем тезис о том,
что эмпирической основой квантовой теории XX века стал периодический
закон химических элементов, открытый в 1869 году великим русским учёным
Д.И. Менделеевым задолго до открытия структуры атома.
Описание истории квантовой механики мы начинаем не с работы
М. Планка 1900 года, как это часто делают, а с гораздо более ранней даты,
с 1 марта 1869 года. В этот день великий русский учёный Д.И. Менделеев на
заседании Русского химического общества доложил об открытии периодиче-
ского закона химических элементов, оформленного в виде таблицы, которая
носит теперь его имя. Периодический закон Менделеева, сформулированный
ещё до открытия структуры атома, стал эмпирической основой, путеводной
нитью квантовой теории XX-го века.
Замечательно, что Д.И. Менделеев подробно рассматривал спектры раз-
личных элементов и, в частности, формулу Бальмера для водорода, которая
значительно позже послужила Нильсу Бору эмпирической основой для по-
строения первой квантовой теории атома в 1913 году, через шесть лет после
смерти Менделеева. О спектрах элементов Д.И. Менделеев писал [76]: «В пла-
мени гремучего газа у Ca, Sr, Ba особенно выступают по одной резкой (яркой)
линии, а именно для Ca – линия 422,7, для Sr – 460,8 и для Ba – 553,6. Там и
тут с повышением веса атома изменение идет в сторону красного конца спек-
тра. Во всех подобных сопоставлениях виден зачаток понимания связи между
атомными весами, химическими аналогиями и положением спектральных
линий простых тел, но, по моему мнению, ещё не видно тех точных законно-
стей, которые управляют зависимостью указанных предметов, а видно лишь
отражение периодического закона».
Точные законности, о которых мечтал Менделеев, связывающие Перио-
дическую таблицу элементов с положением спектральных линий, были обна-
ружены Мозли в том же 1913 году [77, 78], в котором Н. Бор предложил свою
квантовую модель атома. Заметим, что Мозли сделал это в рамках формулы
Бальмера, о которой упоминал Менделеев (точнее в рамках обобщённой
формулы Ридберга – Бальмера).
Впоследствии Нильс Бор писал, что нельзя не восхищаться «интуицией
Менделеева, когда стало видно, что все его предсказания относительно недо-
стающих элементов, а также его предвидения, касающиеся правильной по-
следовательности таких пар элементов, которые были переставлены им при
классификации по возрастающему атомному весу, подтверждены работами
Мозли» [79].
После открытия периодического закона в 1869 году Д. И. Менделеев
два года совершенствовал его формулировку и окончательно сформулировал
свой закон в 1871 году в следующем виде: «Свойства элементов, а потому и
свойства образуемых ими простых и сложных тел, стоят в периодической за-
висимости от их атомного веса».
На основании предположения, что атомная масса предопределяет свой-
ства элемента, Менделеев взял на себя смелость изменить принятые атом-
ные веса некоторых элементов и подробно описать свойства не открытых ещё
элементов. Д. И. Менделеев на протяжении многих лет боролся за признание
периодического закона. Его идеи получили всеобщее одобрение только после
того, как были открыты предсказанные Менделеевым элементы: экаалюми-
ний, экабор и экасилиций; в современной терминологии это соответствен-
но галлий (Поль Лекок де Буабодран, 1875), скандий (Ларс Нильсон, 1879) и
германий (Клеменс Винклер, 1886). С середины 1880-х годов периодический
закон был окончательно признан в качестве теоретической основы химии.
В этой связи Д.И. Менделеев писал о названных учёных как укрепителях и
утвердителях периодического закона [76].
Как мы понимаем сегодня, с развитием атомной физики и квантовой хи-
мии периодический закон получил более строгую формулировку. Это прои-
зошло благодаря классическим работам Й. Ридберга (1897), А. Ван ден Брука
(1913), Г. Мозли (1913) и др. В результате проведённых исследований был рас-
крыт физический смысл порядкового (атомного) номера элемента. Позднее
была создана квантово-механическая модель периодического изменения
электронного строения атомов химических элементов по мере возрастания
зарядов их ядер (Н. Бор, В. Паули, Э. Шрёдингер, В. Гейзенберг, П. Дирак и
др.). В настоящее время периодический закон Д. И. Менделеева имеет сле-
дующую формулировку: «Свойства химических элементов, а также формы и
32 Введение в квантовые информационные технологии
Глава 1. Квантовая механика и развитие информационных технологий 33
свойства образуемых ими простых веществ и соединений находятся в перио-
дической зависимости от величины зарядов ядер их атомов».
Очень высоко оценивая вклад Менделеева в науку, Нильс Бор в своей
работе [79] говорит о центральной проблеме строения атома, которая «была
поставлена в результате выявления специфической периодичности химиче-
ских свойств элементов, расположенных по возрастающим атомным весам,
о которой с таким энтузиазмом и предвидением говорил Менделеев в своей
фарадеевской лекции в 1889 г.».
Интересно, что Менделеев, ничего не зная о ядрах и их зарядах, тем не
менее хорошо понимал дискретную информационную природу открытого им
периодического закона. Эта дискретность очевидна сегодня, когда мы знаем,
что номер элемента Z – это целочисленный заряд ядра (число протонов), но
это было неочевидно во времена Менделеева. В этой связи Менделеев пишет
[76], что действительный периодический закон не выражает функцию непре-
рывную и мы должны трактовать его так, как поступают в теории чисел, –
прерывно. В частности, пишет Менделеев, между магнием Mg (Z = 12) и алю-
минием Al (Z = 13) не должно быть никаких элементов (разрыв сплошности).
В целом, как пишет Нильс Бор [80], развитие науки «дало полное объ-
яснение замечательных зависимостей между физическими и химическими
свойствами элементов, зависимостей, выраженных в знаменитой таблице
Менделеева. Такое толкование свойств материи казалось осуществлением
античного идеала – свести формулирование законов природы к рассмотре-
нию только чисел, превосходящим даже мечты пифагорейцев».
При моделировании индивидуальных свойств атомных систем мы не-
ожиданно для себя упираемся в непреодолимую стену: возможности даже
перспективных классических суперкомпьютеров оказываются абсолютно
ничтожными по сравнению с уровнем не самых сложных квантовых задач.
Например, для решения уравнения Шрёдингера для атома железа, порядко-
вый номер которого Z = 26, даже с грубой сеткой понадобится число узлов,
сравнимое с числом элементарных частиц во Вселенной.
Выход из тупика предложил Ричард Фейнман, сформулировав в 80-х
годах XX века идею квантовых вычислений [81, 82]. Два ключевых фактора
квантовых вычислительных процессов – это суперпозиция квантовых состо-
яний и квантовая запутанность [2, 83]. Квантовый бит (кубит) обеспечивает
суперпозицию логических состояний на атомарном уровне. С другой сторо-
ны, в силу квантовой запутанности каждый кубит, входящий в состав кван-
тового регистра, теряет свою индивидуальность, приобретая общие свойства
ансамбля. Преимущества квантовых компьютеров в распараллеливании.
Как и природа, квантовый процессор одновременно «перебирает» чрезвы-
чайно большое число альтернатив. На пути создания полномасштабных
квантовых компьютеров встает эффект декогерентизации, рассогласования.
Кубиты неконтролируемо взаимодействуют с окружением, создавая кванто-
вый шум [84].
Основываясь на нашей работе [17], в настоящем разделе мы получаем
оценки необходимых классического и квантового ресурсов (с учётом шу-
мов) для моделирования разных химических элементов, а также оснований
ДНК. В указанной работе [17] было выполнено исследование, направленное
на оценку влияния квантовых шумов на точность решения уравнения Шрё-
дингера в рамках метода Залки – Визнера. Важно отметить, что каждый шаг
эволюции квантового состояния регистра кубитов связан с применением
прямого и обратного преобразования Фурье и, таким образом, точность пре-
образования Фурье в квантовом регистре лимитирует итоговую точность ре-
шения нестационарного уравнения Шрёдингера.
В качестве показателя точности мы рассматриваем вероятность совпаде-
ния F (Fidelity), которая задаётся формулой F = |〈ynoise|ytheor〉|2 и характеризует
степень соответствия между зашумленной волновой функцией ynoise, полу-
ченной методом Залки – Визнера, и точным (но дискретизованным) реше-
нием ytheor.
Проведённый анализ показал, что расчёты вероятности совпадения точ-
ного и зашумлённого решений, выполненные в [17], допускают простую ана-
литическую аппроксимацию:
3
exp 6 (1 ( 1))
32 e o e o F nn mp n
. (1.1)
Здесь ne – число электронов в атоме, совпадающее с зарядом ядра
Z (ne = Z), no – число кубитов на одну координату (в примерах ниже выбира-
лось no = 8, что соответствовало 256 узлам для каждой координаты), m – чис-
ло шагов дискретизации по времени (выбиралось m = 10), pe – вероятность
ошибки в расчёте на одну операцию (рассматривались фундаментальные
по своей природе ошибки, связанные с дефазировкой квантовых состояний).
Относительная ошибка аппроксимации (1.1) в сравнении с более точны-
ми результатами [17] составляет величину порядка 10–4 и ниже.
Заметим, что формула 1.1 даёт только грубую оценку точности, основан-
ную на проведённом исследовании квантового преобразования Фурье, лежа-
щего в основе моделирования квантовых систем методом Залки – Визнера.
Эта формула показывает, что точность моделирования квантовой многоэлек-
тронной системы определяется экспоненциальной функцией, которая бы-
стро спадает с ростом числа электронов, числа кубитов на одну координату,
числа шагов дискретизации по времени, а также с ростом вероятности ошиб-
ки в расчёте на одну операцию.
Из представленной формулы непосредственно следует выражение
для критической вероятности ошибки в отдельной операции:
ln
3
6 (1 ( 1))
32
e
e o o
F
p
n nm n
. (1.2)
34 Введение в квантовые информационные технологии
35
Формула (1.2) в терминах вероятности ошибки pe задаёт уровень требова-
ний к технологии, который необходимо достичь для обеспечения заданной
точности F (в приводимых примерах выбиралось F = 0,9).
При рассмотрении многоэлектронных атомов число учитываемых сте-
пеней свободы составляет 3ne (по три координаты для каждого электрона).
При рассмотрении химических соединений (молекул) необходимо рас-
смотреть движение не только электронов, но и ядер. Здесь число внутрен-
них степеней свободы оценивалось как 3(ne + nn) – next, где ne и nn есть число
электронов и ядер соответственно, next – число внешних степеней свободы,
связанных с поступательным движением и вращением молекулы как цело-
го (предполагалось, что внешние (по существу классические) степени сво-
боды не учитываются в уравнении Шрёдингера); при этом next = 3 для ато-
мов, next = 5 для двухатомных молекул и next = 6 для молекул с числом атомов
3 и более. Заметим, что для обобщения формул 1.1 и 1.2 на случай много-
атомных молекул нужно заменить число электронных степеней свободы
атома, равное 3ne, на число внутренних степеней свободы молекулы, равное
3(ne + nn) – next.
Разработанная модель позволяет задолго до создания полномасштабных
квантовых компьютеров получить прогноз точности с учётом шумов для рас-
чёта на квантовом компьютере химических элементов Периодической си-
стемы Д.И. Менделеева, а также химических соединений. В таблице 1.1
для некоторых химических элементов представлено сравнение необходимых
классического и квантового ресурсов, а также предельно допустимый уро-
вень ошибки в квантовых операциях (для каждой координаты используется
8 кубитов – 256 узлов).
Таблица 1.1. Сравнение необходимых классического и квантового ресурсов для моде-
лирования различных элементов
Элемент
Порядковый
номер Z
Необходимый
классический ресурс
(число ячеек памяти)
Число
кубитов
Критическая
вероятность
ошибки квантовых
операций
Гелий 2 2.8147e+14 48 6.63e-05
Литий 3 4.7224e+21 72 4.42e-05
Бериллий 4 7.9228e+28 96 3.31e-05
Бор 5 1.3292e+36 120 2.65e-05
Углерод 6 2.2301e+43 142 2.21e-05
Азот 7 3.7414e+50 168 1.89e-05
Кислород 8 6.2771e+57 192 1.65e-05
Железо 26 6.9617e+187 624 5.10e-06
Серебро 47 3.6462e+339 1128 2.82e-06
Золото 79 5.6607e+570 1896 1.68e-06
Глава 1. Квантовая механика и развитие информационных технологий
В третьем и четвертом столбцах таблицы видно колоссальное преимуще-
ство квантового моделирования по сравнению с классическим. Это эффект,
который характеризует так называемое квантовое превосходство. Для атома
железа потребуется всего 624 кубита вместо классического ресурса порядка
10187 ячеек, который превышает механический ресурс всей Вселенной (число
элементарных частиц (барионов) во Вселенной – «всего» порядка 1078). Ана-
логично для атома золота (Z = 79) потребуется только 1896 кубитов вместо
вместо классического ресурса порядка 10570 ячеек.
Для реализации квантовых вычислений важно радикально подавить
квантовые шумы (столбец 5) до уровня порядка одной ошибки на миллион
операций. Это недоступно для технологий сегодняшнего дня, но, безусловно,
станет возможным в ближайшие десятилетия.
В таблице 1.2 приведено сравнение необходимых классического и кван-
тового ресурсов для моделирования различных оснований ДНК. Из этой та-
Таблица 1.2. Сравнение необходимых классического и квантового ресурсов для моде-
лирования различных оснований ДНК
Аденин А
С5H5N5
Необходимое число кубит – 1992
Критическая вероятность ошибки – 1.6e-06
Необходимый классический ресурс – 4.4849e+599
Цитозин С
С4H5N3O
Необходимое число кубит – 1656
Критическая вероятность ошибки – 1.92e-06
Необходимый классический ресурс – 3.2039e+498
Гуанин G
С5H5N5O
Необходимое число кубит – 2208
Критическая вероятность ошибки – 1.44e-06
Необходимый классический ресурс – 4.7231e+664
Тимин T
С5H6N2O2
Необходимое число кубит – 1896
Критическая вероятность ошибки – 1.68e-06
Необходимый классический ресурс – 5.6607e+570
36 Введение в квантовые информационные технологии
37
блицы мы видим, что для моделирования оснований ДНК, как и тяжёлых
химических элементов в таблице 1.1, нужное число кубитов – порядка 2000 и
опять при низком уровне шума порядка 10–6.
Отметим, что анализ, выполненный в [17], был заведомо приближён-
ным. Исследование было сосредоточено на анализе влияния шумов в кван-
товом преобразовании Фурье на точность решения уравнения Шрёдингера.
Выполненное рассмотрение задачи моделирования уравнения Шрёдингера
на квантовом компьютере отвлекалось от ряда существенных факторов, та-
ких как конечная точность дискретизации, ошибки в фазовых преобразова-
ниях, релятивистские поправки, фермионный характер многоэлектронных
систем и др.
Сейчас мы стоим на пороге второй квантовой революции. В сфере кван-
товых технологий усилия учёных сосредоточены на трёх ключевых направ-
лениях: квантовые коммуникации, квантовые сенсоры и квантовые вычис-
ления. Прототипы квантовых компьютеров последнего времени получили
общее название «NISQ-процессоры» (Noisy Intermediate Scale Quantum –
зашумленные квантовые процессоры промежуточного масштаба).
Вся современная научная деятельность в области квантовой информати-
ки в мире – это большая учебная лаборатория, в которой физики и учёные
других специальностей пытаются освоить основы квантового кода нашей
Вселенной. Когда такое понимание будет достигнуто в должной мере, кван-
товые информационные технологии найдут самое широкое практическое
применение. В этом смысле вся современная квантовая информатика начи-
нается с обучения и имеет своей основной целью получение знаний.
Согласно [2], полномасштабные квантовые компьютеры – это задача
для учёных и инженеров III тысячелетия. Но оно уже наступило. Покорение
огня человеком более двух миллионов лет назад стало первым важнейшим
антропологическим вызовом. Построение устройств квантовой обработки
информации – современный глобальный антропологический вызов, приня-
тие которого для современной цивилизации будет равносильно покорению
огня.
В основе новых технологий лежат квантовые биты информации – куби-
ты. В отличие от классических битов информации, кубиты способны нахо-
диться не только в базисных состояниях «ноль» и «единица», но и в квантовой
суперпозиции этих состояний. Надежды учёных и инженеров связаны с тем,
что квантовые компьютеры, когда они будут созданы, станут незаменимыми
при моделировании квантовых систем, а также при решении других важных
задач, которые недоступны классическим компьютерам.
Создание квантовых технологий обработки информации представляет
собой вызов, стоящий перед человечеством в XXI веке. Эта задача настоль-
ко грандиозна, что через 100 лет изобретение квантовых компьютеров будут
сравнивать с открытием огня. Для решения рассматриваемой задачи в раз-
личных странах, в том числе в России, привлекаются серьёзные интеллекту-
Глава 1. Квантовая механика и развитие информационных технологий
38 Введение в квантовые информационные технологии
альные силы и разрабатываются так называемые дорожные карты, призван-
ные наметить стратегический путь развития таких технологий.
Обсуждение этих и других подобных вопросов начинается с настоящей
главы и продолжается на протяжении всей книги.
1.2. Закон Мура и развитие
информационных технологий
Бурный рост информационных технологий (ИТ) оказывает огромное влия-
ние на жизнь всего современного мирового сообщества. Неуклонно возрас-
тает число людей, работающих в этой области, ИТ широко востребованы
в науке, образовании и промышленности, создаётся глобальное информаци-
онное пространство с использованием сети Интернет, радикально меняются
традиционные концепции телевидения, радио, средств коммуникации и т. п.
Исторический анализ показывает, что информационные технологии ра-
стут экспоненциально быстро. В целом развитие ИТ следует так называемо-
му закону Мура, который основан на эмпирических наблюдениях, сделанных
сотрудником Intel Гордоном Муром ещё на заре интегральной микроэлектро-
ники в 1965 году [85].
Рис. 1.1. Зависимость числа транзисторов в микропроцессорах от времени выпуска.
Прямая демонстрирует удвоение числа транзисторов примерно каждые два года.
Построено по данным компаний Intel (www.intel.com) и AMD (www.amd.com)
Проанализировав развитие микроэлектроники в течение нескольких
первых лет с момента её рождения, Мур представил прогноз, согласно кото-
Глава 1. Квантовая механика и развитие информационных технологий 39
рому число транзисторов в микросхемах будет удваиваться примерно каждые
два года.
Интенсивное развитие микроэлектроники на протяжении последних бо-
лее чем 60 лет вполне соответствует закону Мура. Для иллюстрации на рис. 1.1
представлена зависимость числа транзисторов в микропроцессорах за период
с 1971 по 2017 годы. Представленная зависимость демонстрирует удвоение
числа транзисторов каждые два года.
Фактически экспоненциальному закону Мура приближённо следуют са-
мые различные характеристики полупроводниковых устройств: увеличение
скорости обработки данных, рост объёма памяти, уменьшение критическо-
го размера технологии, снижение стоимости изделия в расчёте на отдельный
транзистор и т. п. Такое экспоненциальное улучшение характеристик прибо-
ров привело к резкому повышению роли микроэлектроники во всех областях
экономики и социальной сферы. В результате информационные технологии
стали локомотивом развития современной цивилизации начиная со второй
половины XX века и по сей день.
Технология суперкомпьютеров и параллельных вычислений также не
стоит в стороне от описываемых тенденций и пытается использовать выгоды,
даваемые законом Мура. Каждый раз, когда на пути дальнейшего увеличения
производительности возникало, на первый взгляд, непреодолимое препят-
ствие, находилось решение, позволяющее его обойти. Например, после того
как тактовая частота процессоров перестала увеличиваться в связи с пробле-
мами отвода тепла, получили широкое распространение многоядерные ар-
хитектуры. В вычислениях стали использоваться графические процессоры,
содержащие многие сотни процессорных ядер.
Заметим, что тенденции, описываемые законом Мура, уже перестали
действовать в последние годы. На фундаментальном уровне предел миниатю-
ризации транзисторов в любом случае ограничен размерами атомов. В част-
ности, существенные трудности, вызванные неконтролируемым квантовым
туннелированием, возникают уже сейчас для затворов размером в 5 нм и ме-
нее. В суперкомпьютерной области дальнейшему экспоненциальному воз-
растанию вычислительной мощности может помешать такое же экспоненци-
альное увеличение потребляемой компьютером электроэнергии.
Заметим, что в настоящее время методы квантовой механики активно
проникают и в разработку способов построения традиционных классических
логических вентилей [86]. Такие системы, построенные на основе твердотель-
ных и молекулярных структур, обеспечивают преобразование информации
посредством квантовых процессов. При этом квантовые аналоги КМОП-
схем строятся на основе быстрых туннельных процессов, а также когерент-
ного транспорта в открытых квантовых системах. Основное препятствие для
создания и широкого использования квантовых логических вентилей такого
рода – это необходимость обеспечения атомарной точности литографиче-
ских процессов.
40 Введение в квантовые информационные технологии
Дальнейший прогресс в области вычислительных технологий, на наш
взгляд, будет связан с тем, что в дополнение к имеющимся технологиям при-
дут новые технологии, такие как оптические, молекулярные и квантовые
компьютеры. Наш нижеследующий рассказ посвящён описанию надежд,
которые исследователи в области квантовых информационных технологий
(КИТ) связывают с квантовыми компьютерами. В настоящее время кван-
товая информатика представляет собой новую быстро развивающуюся от-
расль науки, связанную с использованием квантовых систем для реализации
принципиально новых методов коммуникации и вычислений (квантовые ка-
налы связи, квантовая криптография, квантовый компьютер) [2, 83, 87–91].
Мы увидим, что некоторые основополагающие квантовые эффекты, которые
сейчас зачастую рассматриваются как помеха на пути технологий микро- и
наноэлектроники, могут оказаться источником радикальных новаций в об-
ласти вычислений.
1.3. Блеск и нищета современной физики
По оценке известного американского физика Джона Арчибальда Уилера
(1911–2008 гг.), примерно одна треть ВВП (валового внутреннего продукта)
Соединенных Штатов Америки непосредственно основана на достижениях
квантовой механики. Это и неудивительно, если учесть, что на этой науке
основана практически вся электроника, нанотехнологии, лазерные техноло-
гии, атомная промышленность, новые химические материалы и препараты
и т. п. Успешное развитие указанных отраслей невозможно без проведения
подробных расчётов квантовых систем, таких как наноструктуры, сложные
химические и биологические молекулы, новые лекарства и т. п. Однако, не-
смотря на впечатляющие успехи в изучении фундаментальных законов При-
роды, полномасштабное моделирование сложноорганизованных квантовых
систем всё ещё остаётся практически неосуществимой задачей.
Проиллюстрируем сказанное примером. Для полномасштабного моде-
лирования квантовых свойств атома железа нужно рассматривать движение
всех его 26 электронов в трёхмерном пространстве, что приводит к необхо-
димости решать уравнение Шрёдингера в конфигурационном пространстве
размерности 26 · 3 = 78 (и это без учёта спинов электронов, которые делают
динамику ещё более сложной). Если взять весьма грубую сетку, которая де-
лит каждую координату всего на 10 частей, то понадобится 1078 узлов для ре-
ализации соответствующей разностной схемы. Такого рода моделирование,
однако, никогда не сможет быть осуществлено хотя бы потому, что полное
число элементарных частиц во Вселенной, таких как протоны и нейтроны,
также «всего» порядка 1078. Таким образом, для моделирования всего одного
и далеко не самого сложного атома требуется ресурс, который превышает ме-
ханический ресурс всей Вселенной.
Глава 1. Квантовая механика и развитие информационных технологий 41
Мы видим, что квантовые задачи, за исключением простейших, явля-
ются алгоритмически очень сложными (практически неосуществимыми)
для вычислений на классическом компьютере. Из этого давно известного и,
на первый взгляд, негативного наблюдения Фейнман в 1982 г. сумел сделать
позитивный вывод: раз природа с успехом решает эти задачи, то, может быть,
и мы могли бы использовать квантовые системы в качестве некоторой новой
элементной базы для вычислений. Компьютеры, основанные на квантовых
логических элементах, могли бы быть намного более мощными по сравнению
со своими классическими собратьями. Интересно, что за два года до Фейн-
мана в 1980 г. похожие идеи выдвигал российский математик Юрий Манин
в своей небольшой, но очень содержательной книге «Вычислимое и невы-
числимое» [92].
1.4. Алгоритм Шора и некоторые другие
квантовые алгоритмы
Важным примером, на котором можно продемонстрировать радикальное
преимущество квантовых алгоритмов над классическими, является так назы-
ваемая задача факторизации, связанная с разложением целого числа на про-
стые множители. Оказывается, что в то время как умножение многозначных
чисел – это алгоритмически простая задача, обратная задача (разложение
на множители) алгоритмически очень сложна (обладает экспоненциальной
сложностью для всех известных в настоящее время классических алго-
ритмов).
Наилучший известный на сегодня классический алгоритм факторизации
целого числа (так называемый метод решета числового поля – general number
field sieve) требует для реализации следующее число операций:
exp((64 / 9)1/3 1/3(ln( ))2/3 ), class L n n (1.3)
где n = k log2 10 – число двоичных знаков, а k – число соответствующих деся-
тичных знаков, задающих это число.
Квантовый алгоритм факторизации, предложенный П. Шором в 1994 г.,
требует выполнения числа операций, выражаемым следующей формулой [41]:
2 ln( ) ln(ln( )). quant L n n n (1.4)
Сравнение формул (1.3) и (1.4) показывает, что алгоритм Шора пре-
вращает экспоненциально сложный алгоритм в алгоритм полиномиальной
сложности.
Мы взяли производительность компьютера экзафлопсного диапазона на
уровне 2 · 1018 оп/сек, что несколько превышает производительность двух са-
мых мощных на июнь 2024 года суперкомпьютеров: Frontier (Ок-Риджская
национальная лаборатория США) и Aurora (Аргоннская национальная ла-
42 Введение в квантовые информационные технологии
боратория США). Пересчёт от числа десятичных знаков k к числу двоичных
знаков n осуществлялся по формуле n = k log2 10.
Из таблицы 1.3 видно, что, например, самый мощный на сегодня супер-
компьютер экзафлопсного диапазона (2 · 1018 оп/сек) позволит разложить
число с k = 500 десятичными знаками за 600 миллиардов лет. Ту же задачу
квантовый компьютер мегагерцевого диапазона (1 млн квантовых операций
в секунду) решит за 41 секунду. Аналогично для числа с k = 1000 десятич-
ными знаками трудоёмкость классического алгоритма составляет 3 · 1024 лет,
а квантового – чуть более трёх минут.
Таким образом, квантовой компьютер, когда он будет создан, позволит
решать задачи, которые никогда не сможет решить классический компьютер.
В основе экспоненциального ускорения в алгоритме Шора лежит так
называемое квантовое преобразование Фурье. Для массива комплексных
амплитуд длины N число операций, необходимых для осуществления кван-
тового преобразования Фурье, есть величина порядка O((log N)2). Отметим,
что самые быстрые классические алгоритмы выполняют преобразование
Фурье за O(N(log N)) операций (так называемое быстрое преобразование
Фурье). Таким образом, квантовый алгоритм имеет экспоненциальное пре-
имущество по сравнению со своим классическим аналогом. Пусть, напри-
мер, имеется 1000-кубитовое состояние (n = 1000). Ему отвечает вектор
состояния, описывающийся N = 2n = 1,07 · 10301 комплексными числами.
Для осуществления классического быстрого преобразования потребуется
проделать порядка N log2 N = 1,07 · 10304 операций. В то же время квантовое
преобразование над рассматриваемым вектором осуществляется примерно
за (log2 N)2 = 1 · 106 операций.
Важно отметить следующее. Все известные на сегодня алгоритмы разло-
жения числа на простые множители на классическом компьютере являются
экспоненциально сложными. Если бы удалось доказать, что полиномиаль-
ного алгоритма в задаче факторизации чисел не существует вообще, то тем
самым удалось бы доказать абсолютное превосходство квантовых алгоритмов
над вероятностными классическими. Этот результат установил бы неравен-
ство классов сложности BPP и PSPACE, вопрос о взаимоотношении которых
является одной из ключевых открытых проблем современной теоретической
информатики.
Ещё один важный метод, иллюстрирующий квантовый параллелизм и
имеющий важное методическое значение, даёт алгоритм Дойча – Джозсы.
Суть этого результата заключается в следующем. Рассматривается функция
Таблица 1.3. Классический компьютер экзафлопсного диапазона (2 · 1018 оп/сек)
против квантового компьютера мегагерцевого диапазона (1 млн оп/сек)
Число десятичных знаков k k = 250 k = 500 k = 1000
Трудоёмкость классического алгоритма 140 лет 6 · 1011 лет 3 · 1024 лет
Трудоёмкость квантового алгоритма 9 сек 41 сек 190 сек
Глава 1. Квантовая механика и развитие информационных технологий 43
f (x) с n-битовой областью определения и 1-битовым множеством значений
(n – число кубитов). Переменная x может принимать n различных значе-
ний x = 0, 1, ..., N – 1, где N = 2n. Заранее известно, что функция f(x)может
быть только одного из двух типов: постоянная функция или так называе-
мая сбалансированная функция. Для постоянной функции f(0) = f (1) = ... =
= f(N – 1). Если функция сбалансирована, то f(x) = 0 для некоторых x и
f (x) = 1 для остальных значений аргумента, причём значения f(x) = 0 и
f (x) = 1 встречаются одинаково часто (в этом и заключается сбалансирован-
ность). Пусть, например, имеется функция f (x) с 10-битовой областью опре-
деления. Тогда для некоторых 512 значений x получим f (x) = 0, а для осталь-
ных 512 значений x получим f(x) = 1. Задача Дойча – Джозсы состоит в том,
чтобы отличить постоянную функцию от сбалансированной. Оказывается,
что алгоритм Дойча – Джозсы позволяет с достоверностью решить такую за-
дачу посредством одного-единственного обращения к вычислителю, кото-
рый определяется некоторым унитарным преобразованием Uf . В то же время
при классическом рассмотрении задачи Дойча – Джозсы для того, чтобы с до-
стоверностью отличить постоянную функцию от сбалансированной, может
потребоваться до 2n – 1 + 1 обращений к устройству, производящему вычисле-
ние функции f(x).
В качестве ещё одного замечательного результата стоит упомянуть ал-
горитм Гровера, который направлен на решение задач перебора, например
поиска записи в неструктурированной базе данных. Алгоритм Гровера обе-
спечивает поиск решения за O(√–
N) шагов в базе из N элементов. Заметим,
что классический алгоритм не способен решить задачу быстрее, чем за O(N)
шагов. Фактически при помощи алгоритма Гровера можно получать квадра-
тичное ускорение на NP-полных задачах.
Заметим, что алгоритм Гровера, как и квантовое преобразование
Фурье, смогут найти широкое применение в качестве важнейших состав-
ных частей при моделировании квантовых систем на квантовых компьюте-
рах. В то же время алгоритм факторизации Шора имеет большое значение
для задач криптографии. Создание полномасштабных квантовых компью-
теров и соответствующая реализация алгоритма Шора сделают беззащит-
ными системы классической криптографии с открытым ключом, такие как
RSA-код (назван по фамилиям авторов Р. Ривеста, А. Шамира и Л. Адлемана),
который сейчас используют для защиты информации в банковской
сфере и Интернете.
Таким образом, квантовые компьютеры, когда они будут созданы, позво-
лят решать задачи полномасштабного моделирования сложноорганизован-
ных квантовых систем, недоступные никаким классическим компьютерам,
а также некоторые другие важные задачи.
Важно отметить, что на пути создания квантового компьютера и кван-
товых алгоритмов встаёт множество задач, которые в силу экспоненциаль-
ного роста сложности относительно числа кубитов требуют больших вы-
44 Введение в квантовые информационные технологии
числительных ресурсов. Например, для анализа работы двадцатикубитового
квантового регистра требуется работа с матрицами размера 220×220. Работа
с такими матрицами трудна для современных персональных компьютеров,
однако может быть проделана при помощи суперкомпьютеров. Примеров
успешного применения высокопроизводительных вычислений в квантовой
информатике довольно много. Конечно же, добавление лишь нескольких де-
сятков кубитов поднимает данные задачи на уровень, недоступный никаким
суперкомпьютерам, но это как раз и означает, что использование наиболее
прогрессивных вычислительных технологий является критически важным
фактором для развития КИТ.
1.5. Кубит vs бит (логический анализ)
Основным элементом квантового компьютера является квантовый бит
(кубит), представляющий собой двухуровневую квантовую систему. В ка-
честве кубитов могут выступать ионы, атомы, электроны, фотоны, спины
атомных ядер, структуры из сверхпроводников и многие другие физические
системы. Проведём краткое сравнение кубита с физической реализаци-
ей классического бита информации на основе двоичного триггера с двумя
устойчивыми состояниями.
Так же как и классический бит, кубит может находиться в двух базисных
состояниях – |0〉 и |1〉. Пусть в качестве кубита выступает, например, атом.
Пусть, как показано на рисунке 1.2, |0〉 – это основное состояние, а |1〉 – не-
которое возбуждённое долгоживущее состояние. Именно эти состояния и
образуют кубит. Конечно, кроме указанных состояний у атома есть и мно-
го других состояний (одно из таких состояний, обозначенное как |2〉, пред-
ставлено на рисунке). Однако мы можем сделать так, что все другие воз-
буждённые состояния остаются практически невозмущёнными, если будем
управлять кубитом с помощью лазерного излучения, частота которого близка
к частоте перехода w01 между состояниями кубита |0〉 и |1〉 (только этот пере-
ход оказывается в резонансе с полем лазера, все остальные степени свободы
атома будут практически заморожены). Пусть вначале атом не возбуждён,
т. е. находится в состоянии |0〉. Перевод системы из состояния |0〉 в состоя-
ние |1〉 осуществляется с помощью так называемого p-импульса, который
задаётся посредством выбора длительности импульса лазерного излуче-
ния и напряжённости его электрического поля. Если же атом находится
в возбуждённом состоянии (на уровне |1〉) и на него ещё раз подействовать
p-импульсом, то атом перейдёт обратно в состояние |0〉. Такое поведение пол-
ностью аналогично поведению классического бита и, если бы всё ограничива-
лось этим, то не было бы никакой разницы между классической и квантовой
информацией.
Однако давайте теперь рассмотрим, что произойдёт, если подействовать
на атом не p-импульсом, а импульсом вдвое меньшей длительности, т. е. им-
Глава 1. Квантовая механика и развитие информационных технологий 45
пульсом p/2. В этом случае атом начнёт свой переход из состояния |0〉 в со-
стояние |1〉, но не успеет завершить его. В результате, как оказывается, воз-
никнет состояние квантовой статистической неопределённости, которое мы
можем условно записать как состояние суперпозиции (|0〉 + |1〉)/√–
2. В этой
записи нет ничего таинственного. Она означает, что кубит может с вероятно-
стью 1/2 оказаться в состоянии |0〉 и с такой же вероятностью 1/2 – в состоя-
нии |1〉 (см. ниже). Здесь 1/√–
2 – амплитуда вероятности, а вероятность, в со-
ответствии с законами квантовой механики, есть квадрат модуля амплитуды.
Такое поведение кубита обусловлено его фундаментальной информационной
ограниченностью (между показанными на рисунке уровнями |0〉 и |1〉 про-
сто нет никаких «полочек», на которых атом мог бы «остановиться» по пути
от одного состояния к другому).
Как хорошо известно, поведение классического бита информации со-
всем другое. Например, в микросхемах на основе транзисторно-транзи-
сторной логики (ТТЛ) логический ноль представляется определённым низ-
ким напряжением в диапазоне от нуля до 0,8 В, в то время как логическая
единица – определённым уровнем высокого напряжения в диапазоне от 2,4
до 5,0 В. При этом, конечно, в системе физически возможны и любые другие
промежуточные значения напряжения между логическими нулём и едини-
цей, которые фактически отвечают неисправности схемы. В отличие от кван-
тового бита, классический бит представляет собой физическую систему
с практически неограниченным числом степеней свободы и состояний, сре-
ди которых условно выбираются «ноль» и «единица». Таким образом, самое
главное (и фундаментальное) отличие кубита от классического бита состоит
в том, что в основе первого лежит естественное квантование информации,
в то время как в основе второго – искусственная дискретизация аналогового
сигнала.
Информационная ограниченность квантовых систем приводит к необ-
ходимости их статистического описания. Согласно квантовой механике, со-
стояние физической системы задаётся с помощью таких объектов, как вол-
новая функция и матрица плотности, которые, образно говоря, составляют
«полный каталог знаний», позволяющий правильно рассчитать вероятности
Рис. 1.2. Квантовый бит (кубит) на примере энергетических уровней атомов
46 Введение в квантовые информационные технологии
исходов любых будущих измерений. Важно отметить, что статистическая
неопределённость квантовых систем, в отличие от классических, является
управляемой. Так, упомянутое выше состояние (|0〉 + |1〉)/√–
2 не несёт в себе
никакой энтропийной неопределённости. Энтропия этого состояния оказы-
вается равной нулю, поскольку посредством преобразования p/2 (либо, что
то же самое, 3p/2) оно может быть обратно приведено в состояние «ноль».
Такое управление было бы невозможно, если бы мы имели просто класси-
ческую ситуацию, когда половина представителей ансамбля находятся в со-
стоянии «ноль», а половина – в состоянии «единица». В классическом слу-
чае вероятность является субъективной, поскольку исследователь просто
«не знает» «истинного» состояния дел.
Заметим, что безэнтропийными являются все так называемые чистые со-
стояния. Любое такое состояние можно посредством вполне определённого
обратимого унитарного преобразования привести в состояние «ноль». Любое
чистое состояние может быть задано посредством вектора состояния (волно-
вой функции) в гильбертовом пространстве. Представленные выше обозна-
чения, введённые Дираком, такие как |0〉, |1〉, (|0〉 + |1〉)/√–
2 и т. п., как раз дают
примеры векторов квантовых состояний. При этом состояния логического
нуля и единицы оказываются ортогональными друг другу: 〈0|1〉 = 0. Фунда-
ментальное правило, открытое Борном и фон Нейманом и определяющее
статистический аспект квантовой теории, гласит, что вероятность обнару-
жить систему в состоянии |j〉 при условии, что она была приготовлена в со-
стоянии |y〉, задаётся квадратом модуля их скалярного произведения:
F = | 〈j|y〉 |2. (1.5)
Введённая величина F называется степенью согласованности или ве-
роятностью совпадения квантовых состояний fidelity. Если, например,
|y〉 = (|0〉 + |1〉)/√–
2 , а |j〉 = |0〉, то 〈j|y〉 = 1/√–
2 и F = 1/2.
Заметим, что наряду с чистыми состояниями существуют и так называ-
емые смешанные состояния, описываемые в рамках формализма матрицы
плотности и соответствующие некогерентным смесям чистых состояний
(см. раздел 2.3). Смешанные состояния обладают энтропией, которую можно
вычислить по формуле фон Неймана:
2 log . j j
j
S (1.6)
Эта формула является квантовым аналогом известной формулы Шенно-
на (причём, в роли вероятностей выступают собственные значения матри-
цы плотности lj). Заметим, однако, что исторически формула фон Нейма-
на возникла раньше, в 1932 г., в то время как Шеннон ввёл свою энтропию
только в 1948 г. Более того, по свидетельству Шеннона, сама идея исполь-
зовать термин «энтропия» была подсказана ему фон Нейманом в частной
беседе.
Глава 1. Квантовая механика и развитие информационных технологий 47
Смешанные состояния несут в себе ненулевую энтропию, обусловлен-
ную информационной связью квантовой системы с её окружением. Эта связь
приводит к своеобразному «уходу» информации из системы в окружение,
в результате теряется квантовая когерентность системы и возможность авто-
номного управления её состоянием. Фактически вместо состояния собствен-
но исходной квантовой системы возникает единое состояние более крупного
объекта «система + окружение» (этим состоянием, однако, зачастую трудно
или даже невозможно управлять практически).
1.6. Представление состояния кубита
на сфере Блоха
Квантовое состояние кубита представляет собой суперпозицию двух базис-
ных состояний физической системы:
0
0 1 0 1
1
1 ,
1 0
0
0 1
c
c c c c
c
(1.7)
где условие |c0|2 + |c1|2 = 1 задаёт нормировку на единицу полной вероятности
состояния кубита.
Рис. 1.3. Кубит на сфере Блоха
Оказывается, что всё множество квантовых состояний кубита можно на-
глядно представить на так называемой сфере Блоха, очень похожей на гло-
бус. Каждое чистое однокубитовое состояние задаётся точкой на сфере Бло-
ха, положение которой определяется полярным q и азимутальным j углами
(рис. 1.3):
48 Введение в квантовые информационные технологии
cos exp
2 2
sin exp
2 2
i
i
. (1.8)
Кубит «живёт» одновременно в абстрактном двумерном гильбертовом
пространстве и в обычном трёхмерном евклидовом пространстве. Вычисли-
тельные операции задаются посредством унитарных вращений на сфере Бло-
ха. Оператор унитарных вращений на угол q относительно единичной оси n→
определяется следующей формулой:
( ) exp( ) cos sin ,
2 2 2 nR i n I i n
(1.9)
где s→ = (s1, s2, s3) – матрицы Паули, I – единичная матрица.
Параметры вращения на сфере Блоха (направление оси вращения и вели-
чина угла поворота) задаются теми физическими воздействиями, которые мы
оказываем на квантовый объект (напряжённостями полей, частотами, поля-
ризациями, длительностью воздействий и т. п.). Аналогичное утверждение
справедливо не только для отдельного кубита, но и для регистра из n кубитов
(только теперь гильбертово пространство имеет размерность 2n).
Таким образом, каждой точке сферы Блоха соответствует некоторое со-
стояние кубита и каждому состоянию кубита – некоторая точка на сфере
Блоха. Например, состояние |0〉 соответствует северному полюсу, а состоя-
ние |1〉 – южному полюсу. При воздействии p/2-импульса на невозмущённый
атом кубит движется от северного полюса до экватора вдоль некоторого ме-
ридиана (например, на рис. 1.3 происходит вращение вокруг оси y).
Заметим, что если бы мы взяли импульс не p/2, а ещё вдвое короче,
т. е. p/4, то кубит в процессе своей эволюции остановился бы не на экваторе,
а на широте 45 градусов в северном полушарии, а если бы мы взяли импульс
3p/4, то оказались бы уже в южном полушарии на широте 45 градусов, и т. д.
Вообще всегда можно подобрать некоторое воздействие на кубит, которое
переведёт его из одной произвольно заданной точки на сфере Блоха в любую
другую, наперёд заданную. Все преобразования такого рода принято называть
унитарными вращениями. С помощью таких вращений можно осуществлять
«навигацию» кубита на сфере Блоха (например, мы можем направить его
из точки с координатами Москвы в точку с координатами Рио-де-Жанейро).
Но следует помнить, что эта красивая картинка – только визуализация
неопределённости квантового состояния. Как бы ни двигался кубит по гло-
бусу, придуманному Блохом, при стандартном измерении он всё равно в кон-
це концов окажется либо на северном полюсе, либо на южном. Чем ближе
кубит к северному полюсу, тем вероятнее, что при измерении он будет об-
наружен в состоянии |0〉, а чем ближе он к южному полюсу, тем вероятнее,
Глава 1. Квантовая механика и развитие информационных технологий 49
что он будет обнаружен в состоянии |1〉. В результате измерения происходит
так называемый квантовый скачок. И где бы ни находился кубит, в результате
квантового скачка он всегда оказывается на полюсе (северном или южном).
1.7. Квантовое измерение и квантовый
скачок
Измерение является весьма сильным стрессовым воздействием на квантовую
систему. Рассмотрим эту операцию на примере типичных измерений в ато-
мах. Вспомним, что наряду с кубитовыми состояниями |0〉 и |1〉 у атома име-
ется и много других состояний. Рассмотрим одно из них, которое на рис. 1.2
обозначено как |2〉. Удобно в качестве уровня |2〉 выбрать такой, который,
в отличие от уровня |1〉, является не долгоживущим, а короткоживущим.
Это означает, что атом, оказавшись на этом уровне, долго там не задержи-
вается, а весьма быстро перескакивает в основное состояние |0〉 (при таком
перескоке, конечно, излучается фотон, который уносит имевшуюся у атома
энергию возбуждения). До сих пор существование этого состояния не имело
для нас решительно никакого значения, поскольку лазерное поле, которое
мы использовали, было резонансным только по отношению к переходу меж-
ду состояниями |0〉 и |1〉, а все другие состояния атома для этого поля практи-
чески не существовали. Но теперь давайте сделаем активным переход между
уровнями |0〉 и |2〉. Для этого используем лазерное излучение соответству-
ющей частоты, близкой к частоте w02 этого перехода. Теперь атом получает
возможность активно эволюционировать между состояниями |0〉 и |2〉. Если
уровень |0〉 окажется заселён, то новое лазерное поле неизбежно приведёт
к заселению и уровня |2〉, но поскольку время жизни на этом уровне мало,
атом быстро излучит фотон в случайном направлении в пространстве и снова
скатится на уровень |0〉, откуда под действием того же лазерного поля снова
поднимется вверх, снова излучит фотон и снова скатится вниз (и так много
раз подряд, в результате получится, что атом «засветится» – это явление на-
зывается лазерной флуоресценцией).
А теперь давайте вспомним, что до измерения атом находился ни в со-
стоянии |0〉, ни в состоянии |1〉, а в некотором состоянии квантовой стати-
стической неопределённости (суперпозиции), которое мы описали ранее.
Теперь, после того как мы сделали активным переход между состояниями |0〉
и |2〉, атом не может больше находиться в состоянии «задумчивости», он вы-
нужден сделать выбор между двумя несовместимыми альтернативами: либо
свалиться в состояние |0〉 и начать активно флуоресцировать, либо «спрятать-
ся» от внешнего лазерного воздействия в состоянии |1〉, которое нечувстви-
тельно к прилагаемому лазерному полю. В результате кубит, находящийся
в произвольной точке сферы Блоха, вынужденно совершит квантовый ска-
чок и окажется либо на северном полюсе (в состоянии |0〉), либо на южном
50 Введение в квантовые информационные технологии
полюсе в состоянии |1〉. При этом если кубит осуществлял свою «навигацию»
в северном полушарии, то, скорее всего, с вероятностью более 50% в соответ-
ствии с формулой (1.5) в результате квантового скачка он окажется на север-
ном полюсе, а если он был в южном полушарии, то, скорее всего, окажется
на южном полюсе (конечно, не исключено, что кубит из широт северного
полушария окажется на южном полюсе и, наоборот, кубит из широт южного
полушария окажется на северном полюсе, но вероятность такого рода про-
цессов заведомо ниже 50%).
Таким образом, имеет место своеобразный «закон инерции квантовой
информации», согласно которому «всякая квантовая система продолжает
удерживаться в своём состоянии квантовой статистической неопределённо-
сти, пока и поскольку информационное воздействие со стороны окружения
не понуждает её сделать выбор между различными альтернативами в пользу
какой-то одной». В нашем примере, пока переход между состояниями |0〉 и |2〉
не был освещён, атому не было никакой нужды выбирать между |0〉 и |1〉, по-
этому он мог бы находиться очень долго в состоянии «задумчивости» и «не-
решительности»: что выбрать – |0〉 или |1〉? Но как только переход |0〉 → |2〉
был освещён ярким светом, ему пришлось выбирать: либо быть в нуле,
тогда нужно светиться, флуоресцировать, либо же «прятаться» на «тём-
ной» энергетической полке |1〉, нечувствительной к лазерному излучению
с частотой w02.
1.8. Системы кубитов и квантовая
запутанность
Однокубитовое состояние (1.7) имеет в своей основе два базисных состояния
(|0〉 и |1〉). У системы из двух кубитов таких базисных состояний уже четыре:
|00〉, |01〉, |10〉, |11〉. Запись |01〉, например, означает, что первый кубит находит-
ся в состоянии «ноль», а второй – в состоянии «единица» и т. д.
Система из двух кубитов может находиться не только в каждом из четы-
рех базисных состояний, но и в состояниях, представляющих собой суперпо-
зиции базисных:
|y〉 = c00|00〉 + c01|01〉 + c10|10〉 + c11|11〉. (1.10)
Неожиданным с точки зрения обычной интуиции является то, что состо-
яние системы не всегда описывается в терминах состояния отдельных её ча-
стей. Например, такое состояние из двух кубитов, как (|00〉 + |11〉)/√–
2, не мо-
жет быть разложено отдельно на состояния каждого из двух кубитов. Другими
словами, мы не можем найти такие комплексные числа a1, b1, a2, b2, которые
обеспечивали бы выполнение следующего равенства:
(a1 |0〉 + b1 |1〉) ⊗ (a2 |0〉 + b2 |1〉) = |00〉 + |11〉. (1.11)
С 90-х годов прошлого века активно развиваются квантовые информаци-
онные технологии, мотивируемые перспективой создания вычислительных
устройств принципиально нового типа с характеристиками, которые недо-
ступны классическим аналогам. В настоящее время в таких устройствах –
квантовых компьютерах и симуляторах – уже продемонстрированы примеры
их превосходства перед классическими компьютерами и появились первые
коммерческие образцы квантовых вычислителей, но пока что с довольно
ограниченными возможностями.
В представляемой читателям книге, рассчитанной на научных работ-
ников, а также аспирантов и студентов, наряду с традиционными методами
квантовой информатики рассматривается и ряд новых подходов, основан-
ных на оригинальных методах и разработках авторов. На мой взгляд, мето-
ды, представленные в книге, весьма интересны и полезны как с фундамен-
тальной, так и с практической точек зрения. Этому во многом способствует
её структура. В первой части представлены общие сведения, составляющие
основу квантовой механики и теории информации, обычно читаемые в соот-
ветствующих разделах университетских курсов физики. Несомненный фун-
даментальный интерес представляет предложенный авторами во второй части
книги симбиоз квантовых и статистических закономерностей, рассматривае-
мый в рамках так называемой шестой проблемы Гильберта, связанной с акси-
оматизацией теории вероятностей. В изложении авторов основой для такой
аксиоматизации, по существу, является математическая модель квантовой те-
ории. Авторы обосновывают, что квантовое состояние можно рассматривать
как естественное обобщение понятия статистического распределения. Важ-
но, что квантовое состояние не может быть сведено к одному-единственному
статистическому распределению, а описывает одновременно совокупность
различных взаимно-дополнительных распределений. Квантовые измерения
таких взаимно-дополнительных распределений лежат в основе методов то-
мографии квантовых состояний и процессов, подробно рассматриваемых
в книге.
Согласно меткому афоризму Людвига Больцмана, «нет ничего практич-
нее, чем хорошая теория». Это целиком относится и к содержанию настоя-
щей книги. Основываясь на глубоком развитии теории, авторы, являющи-
еся сотрудниками Физико-технологического института им. К.А. Валиева
РАН, активно осуществляют разработку методов анализа квантовых систем
и управления ими в задачах контроля качества, стабильности и надежности
систем обработки квантовой информации. Разрабатываемые ими кванто-
вые информационные технологии нацелены на решение проблем, связан-
ных с квантовыми шумами и потерей когерентности квантовых состояний.
14 Введение в квантовые информационные технологии
В основе разрабатываемых авторами подходов лежит оригинальная идея,
связанная с анализом полноты, адекватности и точности реализации кван-
товых вентилей. В своих работах авторы показывают, что математическое
моделирование на базе компьютеров с учётом результатов технологических
и экспериментальных исследований позволяет дать исчерпывающую оценку
качества и эффективности проектируемых и создаваемых систем квантовой
обработки информации, а также сформулировать требования к эксперимен-
тальному оборудованию и технологии. Обращаю внимание, что излагаемые
в книге методы и подходы широко используются в проводимых в настоящее
время экспериментах по построению квантовых вычислительных устройств и
проверке основ квантовой теории. На мой взгляд, эта книга будет интересна
не только физикам, но и математикам, а также представителям других специ-
альностей, активно интересующимся развитием передовых научных направ-
лений и технологий.
Научный руководитель Центра квантовых технологий
физического факультета МГУ,
доктор физико-математических наук, профессор С.П. Кулик
ЧАСТЬ I.
ОСНОВЫ КВАНТОВОЙ
ИНФОРМАТИКИ
ВВЕДЕНИЕ
Век живи – век учись! И ты наконец достигнешь того, что,
подобно мудрецу, будешь иметь право сказать,
что ничего не знаешь.
Козьма Прутков
Инженерные приложения, возникшие на основе квантовой механики, при-
вели во второй половине XX века к технологической революции, которую
сейчас принято называть первой квантовой революцией. Эта технологиче-
ская революция привела к рождению ядерных технологий, а также созданию
транзисторов, лазеров, компьютеров, мобильной связи, Интернета и многого
другого, без чего невозможно представить нашу сегодняшнюю жизнь. Апоге-
ем этой революции, на наш взгляд, стало присуждение Нобелевской премии
по физике в 2000 году за создание основ современных IT-технологий россий-
скому физику Ж. И. Алфёрову совместно с немецким физиком Г. Крёмером и
американским учёным Д. Килби.
Сейчас мир стоит на пороге второй квантовой революции. Её ключе-
вое отличие от первой квантовой революции состоит в том, что если рань-
ше квантовая механика применялась только на уровне «железа» (hardware),
то теперь, в эпоху второй квантовой революции, она оказывается в самой
сердцевине компьютерной логики и программного обеспечения (software).
Логика вычислительных устройств нового типа (квантовых компьютеров) ба-
зируется на применении фундаментальных принципов квантовой механики,
таких как суперпозиция и запутанность квантовых состояний. Компьютеры,
построенные на квантовых принципах, окажутся гораздо эффективнее своих
классических собратьев в решении ряда практически важных классов задач
в области физики, химии, материаловедения, фармацевтики, оптимальных
методов управления, криптографии и др.
Квантовый компьютер представляет собой грандиозный проект, прак-
тическая выгода от которого для общества возможна только в долгосрочной
перспективе [1]. Однако уже сейчас данное направление исследований при-
знаётся обществом очень важным, о чём говорит присуждение Нобелевских
премий по физике в 2012 и 2022 гг. В 2012 году Нобелевская премия по физике
была присуждена французскому физику Сержу Арошу и американскому фи-
зику Дэвиду Вайнленду «за новаторские экспериментальные методы, позволя-
ющие измерять и управлять отдельными квантовыми системами». В 2022 году
Нобелевской премии по физике были удостоены Ален Аспе (Франция),
18 Введение в квантовые информационные технологии
Джон Ф. Клаузер (США) и Антон Цайлингер (Австрия) «за эксперименты
с запутанными фотонами, доказывающие нарушение неравенств Белла и пи-
онерские исследования в квантовой информатике».
Правительства многих стран, в том числе России, финансируют развитие
квантовой отрасли в рамках специальных дорожных карт по квантовым тех-
нологиям. Лидерами по государственной поддержке квантовой отрасли явля-
ются Китай, Европейский союз и США.
В 2019 году правительством РФ на госкорпорацию «Росатом» была возло-
жена ответственность за реализацию дорожной карты, направленной на раз-
витие высокотехнологичной области «Квантовые вычисления». Аналогичная
ответственность за развитие высокотехнологичной области «Квантовые ком-
муникации» была возложена на ОАО «РЖД».
Перспективность квантовых компьютеров обусловлена тем, что некото-
рые вычислительные задачи могут выполняться экспоненциально быстрее
на квантовом процессоре по сравнению с любым современным или перспек-
тивным классическим суперкомпьютером [2]. Следует отметить, что класс
задач, допускающих квантовое ускорение, весьма узок по сравнению с клас-
сом произвольных математических задач [3]. Фундаментальная проблема
заключается в создании высокопроизводительного процессора, способного
выполнять квантовые алгоритмы в экспоненциально большом вычислитель-
ном пространстве. В настоящее время предложены многие десятки различ-
ных физических платформ, на которых могут быть реализованы квантовые
вычисления. Среди наиболее перспективных платформ можно выделить
в том числе системы на основе ионов в ловушках [4–8], системы на основе
атомов в ловушках [9; 10], сверхпроводниковые процессоры [11–13] и фотон-
ные чипы [12].
В 2021 году исследователи из Университета Инсбрука представили де-
монстрационный образец для квантовых вычислений [5], который умеща-
ется в двух 19-дюймовых серверных стойках и представляет собой первый
в мире компактный квантовый компьютер с захваченными ионами, отвечаю-
щий высоким стандартам качества [5].
В январе 2019 года IBM представила новую систему IBM Q System One,
которая является первым коммерческим квантовым компьютером с 20 куби-
тами [11].
Осенью 2019 года группа учёных под руководством Джона Мартини-
са (J. Martinis) из компании Google заявила о достижении так называемо-
го квантового превосходства (quantum supremacy), которое было получено
с использованием квантового процессора Sycamore, состоящего из 53 кубит.
В статье [12], опубликованной в Nature в октябре 2019 года, утверждалось,
что процессор Sycamore выполнил за 200 секунд задание, на которое само-
му мощному на тот момент классическому суперкомпьютеру Summit потре-
бовалось бы 10 тысяч лет. Однако одновременно с публикацией результатов
Google специалисты компании IBM выступили с попыткой их опровержеВведение
19
ния, утверждая, что в такой вычислительной классической системе, как
Summit, рассматриваемая задача может быть решена всего 2,5 дня или даже
быстрее [14].
В декабре 2020 года группа китайских учёных из the University of Science
and Technology of China (USTC) с целью продемонстрировать квантовое пре-
восходство реализовала бозонные выборки на 76 фотонах с помощью фотон-
ного квантового компьютера Jiuzhang [15]. Авторы утверждают, что класси-
ческому современному суперкомпьютеру потребуется 600 миллионов лет
вычислительного времени, чтобы сгенерировать количество отсчётов, кото-
рое их квантовый процессор может сгенерировать за 20 секунд.
Несмотря на интенсивное развитие квантового компьютинга в течение
более тридцати лет, создание полномасштабного квантового компьютера всё
ещё остаётся недостижимой мечтой для современных технологий. Вместе
с тем исследования, выполненные в последние годы, показали, что квантовое
ускорение достижимо в реальной системе и не запрещено никакими скрыты-
ми физическими законами. Можно констатировать, что существенный про-
гресс в области экспериментальных и технологических исследований вселя-
ет реальную надежду на создание в среднесрочной перспективе квантовых
вычислительных устройств, способных решать практически важные задачи.
Достигнутый уровень квантовых информационных разработок провозгла-
шает новую эру NISQ- (Noisy Intermediate Scale Quantum) технологий. Та-
кие технологии сами по себе ещё до создания полномасштабных квантовых
компьютеров открывают новые довольно широкие вычислительные возмож-
ности, которые включают в себя методы оптимизации, машинное обуче-
ние, материаловедение, химию, а также ряд других научных и практических
областей.
Необходимо обеспечить непрерывное совершенствование NISQ-
технологий с тем, чтобы с течением времени открывались бы возможности
для решения всё более сложных задач. Для решения поставленных задач кри-
тически важно разработать систему непрерывного мониторинга и прогнози-
рования характеристик точности и эффективности квантовых информацион-
ных устройств в зависимости от степени их интеграции для вычислительных
задач различной сложности и для различных уровней декогерентизации и
квантовых шумов [16; 17].
Наряду с математическим моделированием квантовых операций и алго-
ритмов необходимо осуществлять их контроль в условиях реального экспери-
мента. Основным инструментом для этих целей служит томография кванто-
вых состояний и процессов [18–24], которая призвана обеспечить интерфейс
между разработкой элементной базы квантовых компьютеров и симуляторов
и её практическим воплощением. Методы численного анализа и статистиче-
ского моделирования с учётом влияния квантовых шумом, а также резуль-
татов технологических и экспериментальных исследований позволяют дать
исчерпывающую оценку качеству и эффективности проектируемых кван-
20 Введение в квантовые информационные технологии
товых регистров, сформулировать требования к экспериментальному обо-
рудованию и технологии; посредством обратной связи развиваемый подход
позволяет наилучшим образом распорядиться имеющимися ресурсами для
оптимизации процесса разработки квантовых информационных технологий.
Заметим, что наряду с томографией активно развиваются методы кван-
тового контроля, направленные на управление динамикой физических про-
цессов на атомном и молекулярном уровнях [25–28]. Это область науки
с многочисленными приложениями, начиная от селективных лазерно-инду-
цированных атомных и молекулярных возбуждений и заканчивая квантовы-
ми вычислениями и управлением химическими реакциями с помощью спе-
циально подобранных лазерных импульсов.
В России наиболее совершенным прототипом квантового процессора на
сегодня (август 2024 г.) является процессор на ионах в ловушках, реализован-
ный в ФИАН на 25 четырехуровневых кудитах (что эквивалентно степени
интеграции в 50 кубитов). Заметим, что кудиты представляют собой перспек-
тивную платформу для масштабируемых квантовых вычислений [29; 30]. Ак-
тивные работы в области элементной базы квантовых информационных тех-
нологий ведутся также в Российском квантовом центре, Центре квантовых
технологий МГУ, в МФТИ, МИСИС и ряде других организаций.
В 2022 году продемонстрирована технология массового производства
спиновых кубитов на кремниевых пластинах диаметром 300 мм с исполь-
зованием ультрафиолетовой 193-нм иммерсионной литографии (Intel) [31].
Эти достижения могут в недалёком будущем вывести кремниевую платформу
в число основных. В России конструкция квантового компьютера на осно-
ве квантовых точек в каналах полевых транзисторов в кремнии была пред-
ложена во ФТИАН им. К.А. Валиева ещё в конце 90-х гг. [32; 33]. В 1998 году
австралийский физик Б. Кейн (B.E. Kane) предложил использовать в каче-
стве кубита ядерный спин одиночного атома фосфора 31P, имплантирован-
ного в бесспиновый кремний 28Si. Очевидно, что это предложение содержит
синтез методов и материалов из магнитного резонанса и микроэлектроники.
В развитие идеи Кейна К.А. Валиев и А.А. Кокин в 1999 году предложили
строить кубит на ансамбле спинов атомов 31P в 28Si, т. е. использовать спины
многих атомов 31P, а не одного атома. Результаты исследований были обобще-
ны в монографии А.А. Кокина [34].
Другая перспективная твердотельная модель – это квантовые компью-
теры на электронных состояниях в квантовых точках в полупроводниковых
структурах. Преимущества этой схемы обусловлены высокой скоростью вы-
полнения логических операций, возможностью измерения состояний от-
дельных кубитов (благодаря более высокой интенсивности сигнала по срав-
нению с отдельными ядерными спинами), более простыми по сравнению
с ЯМР способами управления кубитами, а также тем, что рассматриваемые
устройства могут работать при более высоких температурах, чем твердотель-
ные ЯМР квантовые регистры. Трудности реализации рассматриваемой мо-
Введение 21
дели связаны с жесткими требованиями к технологии изготовления много-
кубитовых регистров, а также малыми временами релаксации электронных
состояний по сравнению с такими же временами для ядерных спинов.
Основой для рассматриваемой модели может служить зарядовый кубит
на сформированной в арсениде галлия квантовой точке, разделенной управ-
ляемым потенциальным барьером с одним электроном [35]. Проведённое
в работе Л.Е. Федичкина, М. Янченко и К.А. Валиева численное моделиро-
вание показало, что в рассматриваемом случае низкие температуры (~ 1 мК)
обеспечивают исходную инициализацию и требуемую когерентность. В каче-
стве логических состояний «ноль» и «единица» могут служить локализован-
ные состояния электрона в минимумах потенциала при достаточно большой
высоте потенциального барьера. Теоретический анализ доказал возможность
реализации в рассматриваемой модели квантовых однокубитовых, а также
двухкубитовых (например CNOT) операций.
В настоящее время исследования полупроводниковых систем кубитов
проводятся во ФТИАН им. К.А. Валиева и в Институте физики микрострук-
тур РАН.
В препринте [36], опубликованном в апреле 2023 большим авторским
коллективом исследователей Google (более 150 человек), говорится о созда-
нии квантового компьютера Google нового поколения, содержащего 70 ку-
битов. Новый процессор является непосредственным развитием процессора
Sycamore, созданного ещё в 2019 году. Утверждается, что новый квантовый
процессор способен за 6,7 секунд выполнить вычисления, на которые у са-
мого мощного на тот момент суперкомпьютера Frontier ушло бы 47 лет. Во-
прос о степени состоятельности претензий Google на достижение квантового
превосходства с помощью процессора Sycamore первого поколения оставался
актуальной темой научных дискуссий в течение нескольких лет [37]. По мне-
нию исследователей, сомнения о том, достиг ли процессор Google квантового
превосходства, теперь, после создания процессора Sycamore второго поколе-
ния, разрешены в пользу Google.
В 2023 году компания IBM выполнила исследование с использованием
«шумного» квантового процессора Eagle (127 кубит). В том же 2023 году груп-
па исследователей из IBM опубликовала в Nature статью, которая, по мне-
нию авторов, убедительно доказывает практическую полезность квантовых
вычислений [38]. Результаты выполненного эксперимента показывают, что
и до того, как будет обеспечена отказоустойчивость (fault tolerance) кван-
товых схем, полезные результаты можно получать на «шумном» квантовом
компьютере. Авторы отмечают, что квантовые вычисления обещают су-
щественно ускорить решение определённых задач по сравнению с их клас-
сическими «собратьями», однако самым большим препятствием на пути
полномасштабной реализации квантовых вычислений является шум, прису-
щий квантовым информационным системам. Стандартным решением этой
проблемы была бы реализация отказоустойчивых квантовых схем, однако
22 Введение в квантовые информационные технологии
это недостижимо для современного уровня технологии. В экспериментах
на шумном 127-кубитном
процессоре Eagle демонстрируется высокоточное
измерение средних значений (математических ожиданий) в задачах, масштаб
которых многократно превосходит возможности классических вычислений
методом «грубой силы». Авторы не используют методы коррекции ошибок
(error correction), требующие колоссального числа вспомогательных кубитов.
Вместо этого они используют методы «смягчения» ошибок (error-mitigation),
основанные на постобработке результатов квантовых измерений.
В рассмотренной авторами задаче, связанной с моделью Изинга, ради-
кальное преимущество квантового процессора по сравнению с классическим
относится к масштабу задачи: ни один классический компьютер не имеет
столько памяти, чтобы можно было бы закодировать результаты, отвечающие
возможностям 127-го регистра кубитов (заметим, что 2127 = 1.7e + 38).
Заметим также, что эксперимент проводился на 127-кубитном процес-
соре Eagle, а не на более новом процессоре компании Osprey с 433 кубита-
ми, представленном ещё в ноябре 2022 года. Основной причиной сделанно-
го IBM выбора в пользу менее масштабного процессора Eagle является то,
что он уже прошёл третью итерацию улучшений (Revision 3), в то время как
Osprey всё ещё находится на первой экспериментальной итерации. Осущест-
влённые на Eagle модификации привели к увеличению производительно-
сти процессора, а также к снижению уровня шума, что облегчило процедуру
error-mitigation. Важно также иметь в виду, что сама процедура error-mitigation
масштабируется экспоненциально с числом кубитов, поэтому имеющихся
в настоящее время суперкомпьютерных мощностей просто недостаточно для
реализации полномасштабной процедуры error-mitigation на квантовом про-
цессоре Osprey.
Заметим, что в январе 2024 г. в журнале PRX QUANTUM группа иссле-
дователей из США сообщила о точном и эффективном классическом моде-
лировании квантовой системы Изинга на решётке тяжёлых шестиугольни-
ков [39]. Моделирование как раз этой системы было выполнено в 2023 году
на 127-кубитном квантовом процессоре Eagle IBM с использованием ме-
тодов смягчения ошибок для повышения точности [38]. Авторы показали,
что, приняв подход тензорной сети, который отражает геометрию решётки,
можно выполнить классическое моделирование, которое значительно более
полное и точное, чем результаты, полученные с помощью квантового про-
цессора. Авторы также показывают, что их метод позволяет выполнять моде-
лирование системы на длительных временах в термодинамическом пределе,
соответствующем квантовому компьютеру с бесконечным числом кубитов.
По мнению авторов, их подход тензорных сетей имеет более широкое приме-
нение для моделирования динамики квантовых систем такого рода. На наш
взгляд, работы, подобные [39], свидетельствуют об активной разработке но-
вых классических методов и алгоритмов, само появление которых мотивиро-
вано развитием квантовых информационных технологий. Такое соперниче-
Введение 23
ство между классическими и квантовыми алгоритмами несёт несомненную
пользу для обеих отраслей.
О перспективных и неперспективных задачах для квантовых компью-
теров с точки зрения достижения квантового преимущества говорится
в статье [40], опубликованной в мае 2023 года в журнале Communication of
the ACM, представляющем ассоциацию вычислительной техники (ACMAssociation
for Computing Machinery). Отметим, что ACM – старейшая и са-
мая крупная международная организация в компьютерной области, которая
объединяет 83 000 специалистов. Авторы статьи (сотрудники Microsoft) ста-
вят своей целью отделение шумихи вокруг квантовых технологий от прак-
тических задач, в которых возможно реальное достижение квантового
преимущества (quantum advantage). По мнению авторов статьи, многие со-
временные квантовые алгоритмы могут так и не достичь практического
ускорения. В то же время материаловедение и химия имеют огромный по-
тенциал и можно надеяться, что будут изобретены практичные квантовые ал-
горитмы. Из-за ограничений входной и выходной пропускной способности
квантовые компьютеры будут практичны для задач big compute – больших
вычислений с небольшим количеством данных, но не для задач с большим
количеством данных – big data. Квадратичное ускорение, обеспечиваемое
такими алгоритмами, как алгоритм поиска Гровера, недостаточно для прак-
тического квантового преимущества без значительных улучшений всего
программно-аппаратного стека.
В рамках квантовых информационных технологий важное значение име-
ет задача целочисленной факторизации. Для решения данной задачи с помо-
щью стандартных квантовых вычислений используется алгоритм Шора [41].
Однако экспериментальная реализация алгоритма Шора в гейтовом кванто-
вом вычислителе – крайне непростая задача. Например, авторы известной
работы [42] использовали молекулу с семью ядрами со спином 1/2 для фак-
торизации числа 15. Но подобные эксперименты не могут быть применены
для факторизации больших чисел, что приводит к необходимости улучшения
данного алгоритма. Так, в работе [43] предлагается использовать реинициа-
лизируемые кубиты для реализации итеративной вариации алгоритма Шора.
Одним из наилучших результатов при использовании данного алгоритма
остаётся разложение чисел 51 и 85 с помощью квантовой схемы на восьми
кубитах [44]. В течение последних десятилетий было предпринято много по-
пыток реализовать гейтовый алгоритм Шора на различных квантовых вы-
числительных устройствах. Однако квантовые вычисления являются техно-
логией, которая только начинает своё развитие, и существующие квантовые
устройства всё ещё имеют ограниченные возможности и неспособны решать
сложные проблемы, такие как факторизация больших чисел, которые явля-
ются основой криптографических алгоритмов.
В настоящее время активно разрабатываются методы атак на криптогра-
фические алгоритмы, альтернативные подходам с использованием алгоритмов
24 Введение в квантовые информационные технологии
Шора и Гровера. Так, в конце 2022 года группой китайских учёных в препринте
[45] был представлен метод факторизации чисел, совмещающий классический
метод Шнорра [46; 47] и квантовый алгоритм QAOA (Quantum Approximate
Optimization Algorithm – квантовый алгоритм приближенной оптимизации).
Авторы работы утверждают, что разложили с использованием реальных кван-
товых вычислителей самое большое на данный момент 15-значное число
N = 261980999226229 = 15538213 ⋅ 16860433, а также делают оценку, что
с использованием предложенного метода RSA-2048 может быть взломан
на 372 физических кубитах. В связи с последним утверждением работа вы-
звала большой новостной резонанс [48; 49]. Однако профессиональное со-
общество отнеслось к данной работе скептически [50] и стали появляться ра-
боты с указанием конкретных [51] проблем в работе [45]. Сами оригинальные
работы Шнорра вызывают множество вопросов, а предложенный метод не
показал успешной работы на реальных задачах, предложенный же гибридный
метод с использованием алгоритма QAOA данных проблем не разрешает.
Отметим, что в методе Шнорра и соответствующем квантовом расши-
рении задача факторизации чисел сводится к минимизации, что и служит
поводом для использования квантовых вычислителей. Описанная работа
не является первой в данном направлении. Так, например, рассматривались
подходы с использованием квантовых адиабатических алгоритмов [52–54] и
вариационных квантовых алгоритмов [55; 56]. Помимо работы [45] есть и ряд
других работ с факторизацией различных чисел с использованием квантовых
вычислителей [57–60]. Так, в препринте [61] утверждается, что на 10 ионных
кубитах при помощи цифровизованного квантового контрадиабатического
алгоритма было разложено 48-битное число. Однако такие работы имеют ряд
типичных проблем: лишь часть расчётов производится при помощи кванто-
вых вычислителей, выбираются специальные удобные для алгоритмов числа,
представляются нереалистичные оценки масштабируемости. Также стоит от-
метить, что сама возможность получения квантового ускорения при помощи
подобных оптимизационных алгоритмов на данный момент остаётся откры-
тым вопросом.
В январе 2024 г. вышел довольно объёмный препринт (75 стр.), посвя-
щённый оценке преимуществ и рисков, связанных с квантовыми компью-
терами [62]. Работа написана сотрудниками IBM, NIST, Microsoft и ряда
других организаций США и Канады, специализирующихся на квантовых вы-
числениях и информационной безопасности. Авторы препринта отмечают,
что квантовые вычисления — это новая технология, имеющая потенциаль-
но далеко идущие последствия для национального процветания и безопас-
ности. Понимание временных рамок, в течение которых могут проявиться
экономические выгоды и риски национальной безопасности (в частности,
посредством криптоанализа), имеет жизненно важное значение для обеспе-
чения разумного развития этой технологии. Чтобы информировать экспер-
тов по безопасности и лиц, принимающих политические решения по этому
Введение 25
вопросу, авторы, используя имеющуюся на сегодня исследовательскую лите-
ратуру, рассматривают то, что в настоящее время известно о потенциальном
использовании и рисках квантовых компьютеров. Отмечается, что степень
зрелости доступных в настоящее время квантовых компьютеров ещё не до-
стигла такого уровня, чтобы их можно было использовать в производстве
для решения крупномасштабных, промышленно важных задач, и в насто-
ящее время считается, что квантовые компьютеры пока что не представля-
ют угрозу безопасности для классических информационных систем. Вместе
с тем можно выделить две крупномасштабные тенденции — разработку но-
вых приближенных методов (вариационные алгоритмы, смягчение ошибок
и объединение схем), а также коммерческие исследования квантовых прило-
жений, важных для бизнеса. Вместе эти две тенденции могут сделать возмож-
ными полезные и практичные квантовые вычисления в ближайшем будущем.
В то же самое время обсуждаемые новые приближенные методы вряд ли из-
менят необходимые ресурсы для криптоанализа, применяемые к используе-
мым в настоящее время криптосистемам. Анализ существующих и известных
алгоритмов криптоанализа показывает, что они требуют схем, размер которых
превышает те, которые могут быть реализованы современными квантовыми
компьютерами или квантовыми вычислителями, которые могут появиться
в обозримом будущем. Важно отметить, однако, что в литературе встречают-
ся улучшенные квантовые алгоритмы для такого рода задач. Кроме того, риск
для кибербезопасности можно эффективно контролировать за счёт перехода
на новые квантовобезопасные (постквантовые) криптографические прото-
колы. Таким образом, достоверно можно ожидать, что квантовые компью-
теры будут способны выполнять экономически выгодные вычисления, пре-
жде чем они станут пригодны для выполнения операций, которые являются
криптографически релевантными.
Среди новостей последнего времени в области квантовых информацион-
ных технологий отметим следующие.
В марте 2024 года Google совместно с XPRIZE и Женевским форумом
науки и дипломатии (Geneva Science and Diplomacy Anticipator – GESDA)
объявила о запуске трёхлетнего международного конкурса XPRIZE с бюдже-
том в 5 млн. долларов по применению квантовых вычислений для решения
прикладных задач [63]. Конкурс направлен на создание алгоритмов кванто-
вых вычислений, которые можно будет применить на практике (сегодня или
в будущем) для достижения общественно полезных целей, подобных тем, ко-
торые описаны в целях устойчивого развития Организации Объединенных
Наций. Инициаторы отмечают, что конкурс тесно связан со стремлением
квантовой команды Google создать крупномасштабный квантовый компью-
тер с исправлением ошибок и разработкой полезных приложений для кван-
товых вычислений. Таким образом, компания Google заявляет о поддержке
применения новых квантовых технологий для решения крупных задач, име-
ющих глобальный характер.
26 Введение в квантовые информационные технологии
Компания IBM анонсировала аппаратное и программное обеспече-
ние эпохи квантовой полезности, а также дорожную карту до 2033 года [64].
По мнению IBM, эксперимент, описанный ими в июне 2023 года в журнале
Nature [38], изменил существовавший до этого статус-кво. В [38] было проде-
монстрировано, что квантовые компьютеры могут управлять схемами, недо-
ступными для классического моделирования методом «грубой силы». Впер-
вые возникло аппаратное и программное обеспечение, способное выполнять
квантовые схемы без известного априорного ответа в масштабе порядка
100 кубитов и 3000 вентилей. Квантовый компьютер теперь, по мнению IBM,
является вычислительным инструментом, что открывает возможность раз-
вивать науку в областях, выходящих за рамки самих квантовых вычислений.
Из таких крупномасштабных экспериментов стало ясно, что нужно выйти
за рамки традиционных моделей квантовых схем и воспользоваться преиму-
ществами параллелизма в условиях параллельных классических вычислений
и квантовых динамических схем. Появляются новые квантовые алгоритмы,
которые используют несколько потенциально параллельных квантовых схем
с одновременными классическими операциями. Становится очевидным,
что требуется гетерогенная вычислительная архитектура, состоящая из мас-
штабируемого и параллельного выполнения квантовых схем и продвинутых
классических вычислений.
Ещё 4 декабря 2023 г. на ежегодном саммите IBM Quantum Summit
в Нью-Йорке компания IBM представила новейший 133-кубитный кванто-
вый процессор Heron («Цапля») и первый модульный квантовый компьютер
IBM Quantum System Two на его базе. IBM также анонсировала процессор
Condor с 1121 кубитом, который имеет на 50% большую плотность кубитов
по сравнению с IBM Osprey. Как считают в IBM, усилия по созданию этого
устройства открыли путь к масштабированию квантовых вычислений. Про-
цессор Condor является частью долгосрочных исследований IBM по разра-
ботке крупномасштабных квантовых вычислительных систем. Хотя он рас-
полагает огромным количеством кубитов, производительность его сравнима
с 433-кубитным устройством Osprey, представленным в 2022 году. Это связано
с тем, что простое увеличение количества кубитов без изменения архитек-
туры не делает процессор быстрее или мощнее. По мнению представителей
IBM, опыт, полученный при разработке Condor и предыдущих процессоров
(127-кубитного Eagle и 433-кубитного Osprey), проложил путь к прорыву
в перестраиваемой архитектуре на базе процессора Heron. IBM рассматрива-
ет Quantum Heron как самый производительный на сегодняшний день кван-
товый процессор IBM с новой архитектурой, обеспечивающей пятикратное
снижение уровня ошибок.
Квантовая команда IBM возлагает большие надежды на отмеченный
выше вычислитель Quantum System Two, первый модульный квантовый ком-
пьютер компании [65]. По мнению компании, новое устройство представля-
ет собой краеугольный камень квантовоцентрической суперкомпьютерной
Введение 27
архитектуры IBM. Первая такая IBM Quantum System Two, расположенная
в Йорктаун-Хайтс в штате Нью-Йорк, уже начала работу с тремя процессо-
рами IBM Heron и вспомогательной управляющей электроникой. На новом
133-кубитном процессоре IBM Quantum Heron уже проводятся эксперимен-
ты, для выполнения которых IBM предоставляет пользователям доступ через
облако. В число таких пользователей входит Аргонская национальная лабо-
ратория Министерства энергетики США, Токийский университет, Вашинг-
тонский университет, Кёльнский университет, Гарвардский университет и
др. Дополнительные процессоры IBM Heron присоединятся к парку систем
общего назначения IBM в течение 2024 года. IBM продлила дорожную кар-
ту развития IBM Quantum до 2033 года и разработала дорожную карту IBM
Quantum Innovation до 2029 года [66].
В области квантового программного обеспечения 9 марта 2024 г. в соот-
ветствии с планами, озвученными ещё в декабре 2023 г., IBM официально вы-
пустила версию программной среды 1.0 Qiskit [67]. Программная среда Qiskit и
связанный с ней генеративный искусственный интеллект упрощают програм-
мирование квантового компьютера. Кроме того, в целях упрощения процесса
разработки квантовых вычислений IBM анонсирует Qiskit Patterns. Это при-
ложение будет служить механизмом, который позволит квантовым разработ-
чикам легче создавать программный код. Оно основано на наборе инструмен-
тов, позволяющих просто отображать классические задачи, оптимизировать
их для квантовых схем с помощью Qiskit, выполнять эти схемы с помощью
Qiskit Runtime и затем обеспечивать постобработку результатов. С помощью
Qiskit Patterns в сочетании с Quantum Serverless пользователи смогут создавать,
развертывать и выполнять рабочие процессы, интегрирующие классические и
квантовые вычисления в различных средах, таких как облачные или локаль-
ные сценарии. Все эти инструменты предоставят пользователям строительные
блоки, которые позволят легче создавать и запускать квантовые алгоритмы.
В феврале 2024 г. в США открылось первое специализированное пред-
приятие для массового выпуска квантовых компьютеров [68]. Двери завода
компании IonQ были открыты в присутствии делегации от властей штата
Вашингтон. Квантовые компьютеры IonQ выглядят как обычные серверные
стойки, и этим они подкупают заказчиков, среди которых ряд крупнейших
компаний из США и других стран, а также Пентагон. В настоящий момент
компания способна производить и поставлять заказчикам квантовые систе-
мы Forte на 35 алгоритмических кубитах, и в будущем компания запустит
сборку систем Tempo на 64 алгоритмических кубитах. Квантовая платформа
IonQ опирается на кубиты из ионов под управлением лазеров. Такие систе-
мы не требуют криогенного охлаждения или, по крайней мере, охлаждаются
до относительно высоких температур. Это делает работу с ними удобной и
достаточно экономичной по затратам. По утверждению IonQ, когда-нибудь
заводы по производству квантовых компьютеров будут открываться десятка-
ми, но первый останется таким навсегда.
28 Введение в квантовые информационные технологии
В статье, опубликованной в Nature в марте 2024 г. [69], исследователи
из California Institute of Technology (США) выполнили бенчмаркинг точно-
сти и оценку запутанности в смешанных состояниях с помощью 60-атом-
ного аналогового квантового симулятора Ридберга. Рассматривался режим
высокой энтропии запутанности, в котором точное классическое моделиро-
вание становится практически невозможным. Рассматриваемый протокол
сравнительного тестирования включал экстраполяцию результатов сравне-
ний с приближенным классическим алгоритмом с различными пределами
запутанности. Авторы разработали и продемонстрировали систему оценки
экспериментальной запутанности в смешанных состояниях, обнаружив, что
предложенная система способна конкурировать с современными цифровы-
ми квантовыми устройствами, выполняющими эволюцию случайных цепей.
Авторы сравнили экспериментальную точность с точностью, достигнутой
различными приближенными классическими алгоритмами, и обнаружили,
что только предлагаемый ими алгоритм способен адекватно описывать экс-
перимент. По мнению авторов, полученные результаты позволяют создать
новую модель для оценки способности аналоговых и цифровых квантовых
устройств генерировать запутанность в сверхклассическом режиме, что под-
чёркивает разрыв между квантовыми и классическими системами.
Одним из новейших направлений развития квантовых информационных
технологий является квантовый интернет, который развивается на основе
симбиоза квантовых вычислений, квантовых коммуникаций и квантовой
сенсорики. Организационно квантовый интернет представляет собой инфор-
мационную систему, которая объединяет совокупность различных квантовых
устройств в единую глобальную сеть. В качестве соответствующих устройств,
входящих в квантовую сеть, могут выступать различные квантовые процессо-
ры, квантовая память и пр. В качестве информационного ресурса квантово-
го интернета выступают квантовые состояния. Принципиально важно уметь
создавать, передавать, преобразовывать и измерять так называемые запутан-
ные квантовые состояния, способные обеспечивать наличие квантовых кор-
реляций между различными разделёнными в пространстве квантовыми под-
системами.
В качестве базовых технологий квантового интернета могут выступать не
только технологии квантового распределения ключей, но и такие техноло-
гии, как распределённые квантовые вычисления, так называемые квантовые
вычисления «вслепую», сенсорные квантовые сети и пр. Так, распределённые
квантовые вычисления, реализуемые в рамках квантового интернета, обе-
спечивают новые недоступные классическим компьютерам вычислительные
возможности, создаваемые посредством связей между удаленными кванто-
выми узлами. Благодаря функциональным возможностям, предоставляемым
квантовым интернетом, удаленные квантовые устройства могут взаимодей-
ствовать и кооперироваться между собой для решения сложных вычисли-
тельных задач, недоступных для распределенных классических вычислений.
Введение 29
Облачные подходы, при которых пользователи могут удаленно полу-
чать доступ к квантовым серверам, уже стали важной технологией, доступ-
ной современным пользователям, которые могут выполнять вычисления
на коммерчески доступных квантовых вычислительных устройствах. Одна-
ко делегирование квантовых вычислений серверу сопряжено с проблемами
конфиденциальности и безопасности, которые точно так же ограничивают
и классические облачные вычисления. В настоящее время пользователи не
могут скрыть свою работу от сервера или самостоятельно проверить свои ре-
зультаты. Однако примечательно, что законы квантовой физики позволяют
создать технологии квантовых вычислений «вслепую». Новые технологии
могут оставить сервер «слепым» таким образом, что скроются входные, вы-
ходные данные и алгоритм клиента. Поскольку квантовая информация не
может быть скопирована, а измерения необратимо изменяют квантовое со-
стояние, информация, хранящаяся в этих системах, может быть защищена
с помощью квантовой теоретико-информационной безопасности. Важно,
что неправильная работа сервера или попытки атаки могут быть обнаружены
(удивительная возможность, которой нет в классических вычислениях).
В апреле 2024 г. группа исследователей Imperial College London опубли-
ковала в журнале Science Advances статью «Детерминированное хранение
и извлечение телекоммуникационного света из однофотонного источни-
ка на квантовых точках, соединенного с атомной квантовой памятью» [70].
Был реализован гибридный интерфейс твердотельных однофотонных ис-
точников и атомной квантовой памяти, что являлось давней целью фотон-
ных квантовых технологий. Авторы продемонстрировали детерминирован-
ное хранение и извлечение света из полупроводниковой квантовой точки
в квантовой памяти атомного ансамбля на телекоммуникационных длинах
волн. Хранились одиночные фотоны из квантовой точки арсенида индия
в широкополосной квантовой памяти на основе паров рубидия с общей эф-
фективностью внутренней памяти (12,9 ± 0,4)%. Отношение сигнал/шум
полученного светового поля составляло 18,2 ± 0,6 и ограничивалось только
темновыми отсчётами детектора. Заметим, что квантовая память представ-
ляет собой квантово-механическую версию обычной компьютерной памяти.
В то время как обычная память хранит информацию в виде двоичных клас-
сических состояний (представленных в виде 0 и 1), квантовая память хранит
целое квантовое состояние для последующего извлечения. Квантовая память
может использоваться в самых разных областях, включая квантовые вычис-
ления и квантовую связь [71–74].
В статье, опубликованной в апреле 2024 г. в журнале Physical Review
Letters [75], исследователи из University of Oxford (Великобритания) сообща-
ют о первой гибридной вещественно-фотонной (matter-photon) реализации
поддающихся проверке слепых квантовых вычислений. Авторы использова-
ли квантовый сервер захваченных ионов и клиентскую систему фотонного
обнаружения, объединенные в сеть через оптоволоконную квантовую связь.
30 Введение в квантовые информационные технологии
Наличие кубитов памяти и детерминированных шлюзов запутанности позво-
лило использовать интерактивные протоколы без постселекции — ключевое
требование для любого масштабируемого слепого сервера, которое ранее не
могло быть обеспечено. Авторы количественно оценили потерю конфиден-
циальности как ≤ 0,03 утечки классических битов на кубит (Fidelity > 97%).
Выполненный эксперимент, по мнению авторов, демонстрирует путь к пол-
ностью доверенным квантовым вычислениям в облаке.
Важными системами, которые могут быть реализованы в рамках кван-
тового интернета, являются системы квантового позиционирования и кван-
тового определения дальности с помощью распределённой сенсорной сети.
Такого рода системы квантового позиционирования и квантового ориенти-
рования могут быть созданы, в частности, с использованием сетевых радаров
с фазированной решёткой и квантовым усилением на основе квантовых со-
стояний многочастной запутанности в непрерывных переменных. Оказыва-
ется, что использование сенсорной сети для квантового позиционирования
и квантового определения дальности обеспечивает существенное преиму-
щество в точности в трёхмерном пространстве по сравнению с классической
схемой, также существенно увеличивая дальность обнаружения объектов.
Настоящая книга включает в себя 20 глав, сгруппированных в две ча-
сти. В первой части изложены основы квантовой информатики, во второй
части рассматривается приложение методов квантовой информатики к ана-
лизу классических и квантовых систем. Материал книги основан на лекциях,
которые в течение ряда лет читались авторами студентам Центра квантовых
технологий физического факультета МГУ, студентам кафедры квантовой фи-
зики и наноэлектроники Национального исследовательского университе-
та электронной техники (НИУ МИЭТ), а также студентам кафедры физики
конденсированных сред Национального исследовательского ядерного уни-
верситета МИФИ (НИЯУ МИФИ).
Авторы благодарны всем своим коллегам и ученикам за научное сотруд-
ничество в области квантовых технологий. Наша особая признательность
Борису Бантышу, Дмитрию Фастовцу, Андрею Чернявскому, Гранту Авосо-
пянцу, Константину Катамадзе и Юрию Кузнецову за помощь в подготовке
настоящего издания.
ГЛАВА 1.
КВАНТОВАЯ МЕХАНИКА И
РАЗВИТИЕ ИНФОРМАЦИОННЫХ
ТЕХНОЛОГИЙ
Где начало того конца, которым оканчивается начало?
Козьма Прутков
Настоящая глава является вводной. В ней представлен обзор квантовых тех-
нологий обработки информации «с высоты птичьего полёта».
1.1. Менделеев, рождение квантовой
механики и оценка требований
к квантовым компьютерам
8 февраля 2024 года исполнилось 190 лет со дня рождения Д.И. Менделеева.
В настоящем разделе в историческом контексте мы развиваем тезис о том,
что эмпирической основой квантовой теории XX века стал периодический
закон химических элементов, открытый в 1869 году великим русским учёным
Д.И. Менделеевым задолго до открытия структуры атома.
Описание истории квантовой механики мы начинаем не с работы
М. Планка 1900 года, как это часто делают, а с гораздо более ранней даты,
с 1 марта 1869 года. В этот день великий русский учёный Д.И. Менделеев на
заседании Русского химического общества доложил об открытии периодиче-
ского закона химических элементов, оформленного в виде таблицы, которая
носит теперь его имя. Периодический закон Менделеева, сформулированный
ещё до открытия структуры атома, стал эмпирической основой, путеводной
нитью квантовой теории XX-го века.
Замечательно, что Д.И. Менделеев подробно рассматривал спектры раз-
личных элементов и, в частности, формулу Бальмера для водорода, которая
значительно позже послужила Нильсу Бору эмпирической основой для по-
строения первой квантовой теории атома в 1913 году, через шесть лет после
смерти Менделеева. О спектрах элементов Д.И. Менделеев писал [76]: «В пла-
мени гремучего газа у Ca, Sr, Ba особенно выступают по одной резкой (яркой)
линии, а именно для Ca – линия 422,7, для Sr – 460,8 и для Ba – 553,6. Там и
тут с повышением веса атома изменение идет в сторону красного конца спек-
тра. Во всех подобных сопоставлениях виден зачаток понимания связи между
атомными весами, химическими аналогиями и положением спектральных
линий простых тел, но, по моему мнению, ещё не видно тех точных законно-
стей, которые управляют зависимостью указанных предметов, а видно лишь
отражение периодического закона».
Точные законности, о которых мечтал Менделеев, связывающие Перио-
дическую таблицу элементов с положением спектральных линий, были обна-
ружены Мозли в том же 1913 году [77, 78], в котором Н. Бор предложил свою
квантовую модель атома. Заметим, что Мозли сделал это в рамках формулы
Бальмера, о которой упоминал Менделеев (точнее в рамках обобщённой
формулы Ридберга – Бальмера).
Впоследствии Нильс Бор писал, что нельзя не восхищаться «интуицией
Менделеева, когда стало видно, что все его предсказания относительно недо-
стающих элементов, а также его предвидения, касающиеся правильной по-
следовательности таких пар элементов, которые были переставлены им при
классификации по возрастающему атомному весу, подтверждены работами
Мозли» [79].
После открытия периодического закона в 1869 году Д. И. Менделеев
два года совершенствовал его формулировку и окончательно сформулировал
свой закон в 1871 году в следующем виде: «Свойства элементов, а потому и
свойства образуемых ими простых и сложных тел, стоят в периодической за-
висимости от их атомного веса».
На основании предположения, что атомная масса предопределяет свой-
ства элемента, Менделеев взял на себя смелость изменить принятые атом-
ные веса некоторых элементов и подробно описать свойства не открытых ещё
элементов. Д. И. Менделеев на протяжении многих лет боролся за признание
периодического закона. Его идеи получили всеобщее одобрение только после
того, как были открыты предсказанные Менделеевым элементы: экаалюми-
ний, экабор и экасилиций; в современной терминологии это соответствен-
но галлий (Поль Лекок де Буабодран, 1875), скандий (Ларс Нильсон, 1879) и
германий (Клеменс Винклер, 1886). С середины 1880-х годов периодический
закон был окончательно признан в качестве теоретической основы химии.
В этой связи Д.И. Менделеев писал о названных учёных как укрепителях и
утвердителях периодического закона [76].
Как мы понимаем сегодня, с развитием атомной физики и квантовой хи-
мии периодический закон получил более строгую формулировку. Это прои-
зошло благодаря классическим работам Й. Ридберга (1897), А. Ван ден Брука
(1913), Г. Мозли (1913) и др. В результате проведённых исследований был рас-
крыт физический смысл порядкового (атомного) номера элемента. Позднее
была создана квантово-механическая модель периодического изменения
электронного строения атомов химических элементов по мере возрастания
зарядов их ядер (Н. Бор, В. Паули, Э. Шрёдингер, В. Гейзенберг, П. Дирак и
др.). В настоящее время периодический закон Д. И. Менделеева имеет сле-
дующую формулировку: «Свойства химических элементов, а также формы и
32 Введение в квантовые информационные технологии
Глава 1. Квантовая механика и развитие информационных технологий 33
свойства образуемых ими простых веществ и соединений находятся в перио-
дической зависимости от величины зарядов ядер их атомов».
Очень высоко оценивая вклад Менделеева в науку, Нильс Бор в своей
работе [79] говорит о центральной проблеме строения атома, которая «была
поставлена в результате выявления специфической периодичности химиче-
ских свойств элементов, расположенных по возрастающим атомным весам,
о которой с таким энтузиазмом и предвидением говорил Менделеев в своей
фарадеевской лекции в 1889 г.».
Интересно, что Менделеев, ничего не зная о ядрах и их зарядах, тем не
менее хорошо понимал дискретную информационную природу открытого им
периодического закона. Эта дискретность очевидна сегодня, когда мы знаем,
что номер элемента Z – это целочисленный заряд ядра (число протонов), но
это было неочевидно во времена Менделеева. В этой связи Менделеев пишет
[76], что действительный периодический закон не выражает функцию непре-
рывную и мы должны трактовать его так, как поступают в теории чисел, –
прерывно. В частности, пишет Менделеев, между магнием Mg (Z = 12) и алю-
минием Al (Z = 13) не должно быть никаких элементов (разрыв сплошности).
В целом, как пишет Нильс Бор [80], развитие науки «дало полное объ-
яснение замечательных зависимостей между физическими и химическими
свойствами элементов, зависимостей, выраженных в знаменитой таблице
Менделеева. Такое толкование свойств материи казалось осуществлением
античного идеала – свести формулирование законов природы к рассмотре-
нию только чисел, превосходящим даже мечты пифагорейцев».
При моделировании индивидуальных свойств атомных систем мы не-
ожиданно для себя упираемся в непреодолимую стену: возможности даже
перспективных классических суперкомпьютеров оказываются абсолютно
ничтожными по сравнению с уровнем не самых сложных квантовых задач.
Например, для решения уравнения Шрёдингера для атома железа, порядко-
вый номер которого Z = 26, даже с грубой сеткой понадобится число узлов,
сравнимое с числом элементарных частиц во Вселенной.
Выход из тупика предложил Ричард Фейнман, сформулировав в 80-х
годах XX века идею квантовых вычислений [81, 82]. Два ключевых фактора
квантовых вычислительных процессов – это суперпозиция квантовых состо-
яний и квантовая запутанность [2, 83]. Квантовый бит (кубит) обеспечивает
суперпозицию логических состояний на атомарном уровне. С другой сторо-
ны, в силу квантовой запутанности каждый кубит, входящий в состав кван-
тового регистра, теряет свою индивидуальность, приобретая общие свойства
ансамбля. Преимущества квантовых компьютеров в распараллеливании.
Как и природа, квантовый процессор одновременно «перебирает» чрезвы-
чайно большое число альтернатив. На пути создания полномасштабных
квантовых компьютеров встает эффект декогерентизации, рассогласования.
Кубиты неконтролируемо взаимодействуют с окружением, создавая кванто-
вый шум [84].
Основываясь на нашей работе [17], в настоящем разделе мы получаем
оценки необходимых классического и квантового ресурсов (с учётом шу-
мов) для моделирования разных химических элементов, а также оснований
ДНК. В указанной работе [17] было выполнено исследование, направленное
на оценку влияния квантовых шумов на точность решения уравнения Шрё-
дингера в рамках метода Залки – Визнера. Важно отметить, что каждый шаг
эволюции квантового состояния регистра кубитов связан с применением
прямого и обратного преобразования Фурье и, таким образом, точность пре-
образования Фурье в квантовом регистре лимитирует итоговую точность ре-
шения нестационарного уравнения Шрёдингера.
В качестве показателя точности мы рассматриваем вероятность совпаде-
ния F (Fidelity), которая задаётся формулой F = |〈ynoise|ytheor〉|2 и характеризует
степень соответствия между зашумленной волновой функцией ynoise, полу-
ченной методом Залки – Визнера, и точным (но дискретизованным) реше-
нием ytheor.
Проведённый анализ показал, что расчёты вероятности совпадения точ-
ного и зашумлённого решений, выполненные в [17], допускают простую ана-
литическую аппроксимацию:
3
exp 6 (1 ( 1))
32 e o e o F nn mp n
. (1.1)
Здесь ne – число электронов в атоме, совпадающее с зарядом ядра
Z (ne = Z), no – число кубитов на одну координату (в примерах ниже выбира-
лось no = 8, что соответствовало 256 узлам для каждой координаты), m – чис-
ло шагов дискретизации по времени (выбиралось m = 10), pe – вероятность
ошибки в расчёте на одну операцию (рассматривались фундаментальные
по своей природе ошибки, связанные с дефазировкой квантовых состояний).
Относительная ошибка аппроксимации (1.1) в сравнении с более точны-
ми результатами [17] составляет величину порядка 10–4 и ниже.
Заметим, что формула 1.1 даёт только грубую оценку точности, основан-
ную на проведённом исследовании квантового преобразования Фурье, лежа-
щего в основе моделирования квантовых систем методом Залки – Визнера.
Эта формула показывает, что точность моделирования квантовой многоэлек-
тронной системы определяется экспоненциальной функцией, которая бы-
стро спадает с ростом числа электронов, числа кубитов на одну координату,
числа шагов дискретизации по времени, а также с ростом вероятности ошиб-
ки в расчёте на одну операцию.
Из представленной формулы непосредственно следует выражение
для критической вероятности ошибки в отдельной операции:
ln
3
6 (1 ( 1))
32
e
e o o
F
p
n nm n
. (1.2)
34 Введение в квантовые информационные технологии
35
Формула (1.2) в терминах вероятности ошибки pe задаёт уровень требова-
ний к технологии, который необходимо достичь для обеспечения заданной
точности F (в приводимых примерах выбиралось F = 0,9).
При рассмотрении многоэлектронных атомов число учитываемых сте-
пеней свободы составляет 3ne (по три координаты для каждого электрона).
При рассмотрении химических соединений (молекул) необходимо рас-
смотреть движение не только электронов, но и ядер. Здесь число внутрен-
них степеней свободы оценивалось как 3(ne + nn) – next, где ne и nn есть число
электронов и ядер соответственно, next – число внешних степеней свободы,
связанных с поступательным движением и вращением молекулы как цело-
го (предполагалось, что внешние (по существу классические) степени сво-
боды не учитываются в уравнении Шрёдингера); при этом next = 3 для ато-
мов, next = 5 для двухатомных молекул и next = 6 для молекул с числом атомов
3 и более. Заметим, что для обобщения формул 1.1 и 1.2 на случай много-
атомных молекул нужно заменить число электронных степеней свободы
атома, равное 3ne, на число внутренних степеней свободы молекулы, равное
3(ne + nn) – next.
Разработанная модель позволяет задолго до создания полномасштабных
квантовых компьютеров получить прогноз точности с учётом шумов для рас-
чёта на квантовом компьютере химических элементов Периодической си-
стемы Д.И. Менделеева, а также химических соединений. В таблице 1.1
для некоторых химических элементов представлено сравнение необходимых
классического и квантового ресурсов, а также предельно допустимый уро-
вень ошибки в квантовых операциях (для каждой координаты используется
8 кубитов – 256 узлов).
Таблица 1.1. Сравнение необходимых классического и квантового ресурсов для моде-
лирования различных элементов
Элемент
Порядковый
номер Z
Необходимый
классический ресурс
(число ячеек памяти)
Число
кубитов
Критическая
вероятность
ошибки квантовых
операций
Гелий 2 2.8147e+14 48 6.63e-05
Литий 3 4.7224e+21 72 4.42e-05
Бериллий 4 7.9228e+28 96 3.31e-05
Бор 5 1.3292e+36 120 2.65e-05
Углерод 6 2.2301e+43 142 2.21e-05
Азот 7 3.7414e+50 168 1.89e-05
Кислород 8 6.2771e+57 192 1.65e-05
Железо 26 6.9617e+187 624 5.10e-06
Серебро 47 3.6462e+339 1128 2.82e-06
Золото 79 5.6607e+570 1896 1.68e-06
Глава 1. Квантовая механика и развитие информационных технологий
В третьем и четвертом столбцах таблицы видно колоссальное преимуще-
ство квантового моделирования по сравнению с классическим. Это эффект,
который характеризует так называемое квантовое превосходство. Для атома
железа потребуется всего 624 кубита вместо классического ресурса порядка
10187 ячеек, который превышает механический ресурс всей Вселенной (число
элементарных частиц (барионов) во Вселенной – «всего» порядка 1078). Ана-
логично для атома золота (Z = 79) потребуется только 1896 кубитов вместо
вместо классического ресурса порядка 10570 ячеек.
Для реализации квантовых вычислений важно радикально подавить
квантовые шумы (столбец 5) до уровня порядка одной ошибки на миллион
операций. Это недоступно для технологий сегодняшнего дня, но, безусловно,
станет возможным в ближайшие десятилетия.
В таблице 1.2 приведено сравнение необходимых классического и кван-
тового ресурсов для моделирования различных оснований ДНК. Из этой та-
Таблица 1.2. Сравнение необходимых классического и квантового ресурсов для моде-
лирования различных оснований ДНК
Аденин А
С5H5N5
Необходимое число кубит – 1992
Критическая вероятность ошибки – 1.6e-06
Необходимый классический ресурс – 4.4849e+599
Цитозин С
С4H5N3O
Необходимое число кубит – 1656
Критическая вероятность ошибки – 1.92e-06
Необходимый классический ресурс – 3.2039e+498
Гуанин G
С5H5N5O
Необходимое число кубит – 2208
Критическая вероятность ошибки – 1.44e-06
Необходимый классический ресурс – 4.7231e+664
Тимин T
С5H6N2O2
Необходимое число кубит – 1896
Критическая вероятность ошибки – 1.68e-06
Необходимый классический ресурс – 5.6607e+570
36 Введение в квантовые информационные технологии
37
блицы мы видим, что для моделирования оснований ДНК, как и тяжёлых
химических элементов в таблице 1.1, нужное число кубитов – порядка 2000 и
опять при низком уровне шума порядка 10–6.
Отметим, что анализ, выполненный в [17], был заведомо приближён-
ным. Исследование было сосредоточено на анализе влияния шумов в кван-
товом преобразовании Фурье на точность решения уравнения Шрёдингера.
Выполненное рассмотрение задачи моделирования уравнения Шрёдингера
на квантовом компьютере отвлекалось от ряда существенных факторов, та-
ких как конечная точность дискретизации, ошибки в фазовых преобразова-
ниях, релятивистские поправки, фермионный характер многоэлектронных
систем и др.
Сейчас мы стоим на пороге второй квантовой революции. В сфере кван-
товых технологий усилия учёных сосредоточены на трёх ключевых направ-
лениях: квантовые коммуникации, квантовые сенсоры и квантовые вычис-
ления. Прототипы квантовых компьютеров последнего времени получили
общее название «NISQ-процессоры» (Noisy Intermediate Scale Quantum –
зашумленные квантовые процессоры промежуточного масштаба).
Вся современная научная деятельность в области квантовой информати-
ки в мире – это большая учебная лаборатория, в которой физики и учёные
других специальностей пытаются освоить основы квантового кода нашей
Вселенной. Когда такое понимание будет достигнуто в должной мере, кван-
товые информационные технологии найдут самое широкое практическое
применение. В этом смысле вся современная квантовая информатика начи-
нается с обучения и имеет своей основной целью получение знаний.
Согласно [2], полномасштабные квантовые компьютеры – это задача
для учёных и инженеров III тысячелетия. Но оно уже наступило. Покорение
огня человеком более двух миллионов лет назад стало первым важнейшим
антропологическим вызовом. Построение устройств квантовой обработки
информации – современный глобальный антропологический вызов, приня-
тие которого для современной цивилизации будет равносильно покорению
огня.
В основе новых технологий лежат квантовые биты информации – куби-
ты. В отличие от классических битов информации, кубиты способны нахо-
диться не только в базисных состояниях «ноль» и «единица», но и в квантовой
суперпозиции этих состояний. Надежды учёных и инженеров связаны с тем,
что квантовые компьютеры, когда они будут созданы, станут незаменимыми
при моделировании квантовых систем, а также при решении других важных
задач, которые недоступны классическим компьютерам.
Создание квантовых технологий обработки информации представляет
собой вызов, стоящий перед человечеством в XXI веке. Эта задача настоль-
ко грандиозна, что через 100 лет изобретение квантовых компьютеров будут
сравнивать с открытием огня. Для решения рассматриваемой задачи в раз-
личных странах, в том числе в России, привлекаются серьёзные интеллекту-
Глава 1. Квантовая механика и развитие информационных технологий
38 Введение в квантовые информационные технологии
альные силы и разрабатываются так называемые дорожные карты, призван-
ные наметить стратегический путь развития таких технологий.
Обсуждение этих и других подобных вопросов начинается с настоящей
главы и продолжается на протяжении всей книги.
1.2. Закон Мура и развитие
информационных технологий
Бурный рост информационных технологий (ИТ) оказывает огромное влия-
ние на жизнь всего современного мирового сообщества. Неуклонно возрас-
тает число людей, работающих в этой области, ИТ широко востребованы
в науке, образовании и промышленности, создаётся глобальное информаци-
онное пространство с использованием сети Интернет, радикально меняются
традиционные концепции телевидения, радио, средств коммуникации и т. п.
Исторический анализ показывает, что информационные технологии ра-
стут экспоненциально быстро. В целом развитие ИТ следует так называемо-
му закону Мура, который основан на эмпирических наблюдениях, сделанных
сотрудником Intel Гордоном Муром ещё на заре интегральной микроэлектро-
ники в 1965 году [85].
Рис. 1.1. Зависимость числа транзисторов в микропроцессорах от времени выпуска.
Прямая демонстрирует удвоение числа транзисторов примерно каждые два года.
Построено по данным компаний Intel (www.intel.com) и AMD (www.amd.com)
Проанализировав развитие микроэлектроники в течение нескольких
первых лет с момента её рождения, Мур представил прогноз, согласно кото-
Глава 1. Квантовая механика и развитие информационных технологий 39
рому число транзисторов в микросхемах будет удваиваться примерно каждые
два года.
Интенсивное развитие микроэлектроники на протяжении последних бо-
лее чем 60 лет вполне соответствует закону Мура. Для иллюстрации на рис. 1.1
представлена зависимость числа транзисторов в микропроцессорах за период
с 1971 по 2017 годы. Представленная зависимость демонстрирует удвоение
числа транзисторов каждые два года.
Фактически экспоненциальному закону Мура приближённо следуют са-
мые различные характеристики полупроводниковых устройств: увеличение
скорости обработки данных, рост объёма памяти, уменьшение критическо-
го размера технологии, снижение стоимости изделия в расчёте на отдельный
транзистор и т. п. Такое экспоненциальное улучшение характеристик прибо-
ров привело к резкому повышению роли микроэлектроники во всех областях
экономики и социальной сферы. В результате информационные технологии
стали локомотивом развития современной цивилизации начиная со второй
половины XX века и по сей день.
Технология суперкомпьютеров и параллельных вычислений также не
стоит в стороне от описываемых тенденций и пытается использовать выгоды,
даваемые законом Мура. Каждый раз, когда на пути дальнейшего увеличения
производительности возникало, на первый взгляд, непреодолимое препят-
ствие, находилось решение, позволяющее его обойти. Например, после того
как тактовая частота процессоров перестала увеличиваться в связи с пробле-
мами отвода тепла, получили широкое распространение многоядерные ар-
хитектуры. В вычислениях стали использоваться графические процессоры,
содержащие многие сотни процессорных ядер.
Заметим, что тенденции, описываемые законом Мура, уже перестали
действовать в последние годы. На фундаментальном уровне предел миниатю-
ризации транзисторов в любом случае ограничен размерами атомов. В част-
ности, существенные трудности, вызванные неконтролируемым квантовым
туннелированием, возникают уже сейчас для затворов размером в 5 нм и ме-
нее. В суперкомпьютерной области дальнейшему экспоненциальному воз-
растанию вычислительной мощности может помешать такое же экспоненци-
альное увеличение потребляемой компьютером электроэнергии.
Заметим, что в настоящее время методы квантовой механики активно
проникают и в разработку способов построения традиционных классических
логических вентилей [86]. Такие системы, построенные на основе твердотель-
ных и молекулярных структур, обеспечивают преобразование информации
посредством квантовых процессов. При этом квантовые аналоги КМОП-
схем строятся на основе быстрых туннельных процессов, а также когерент-
ного транспорта в открытых квантовых системах. Основное препятствие для
создания и широкого использования квантовых логических вентилей такого
рода – это необходимость обеспечения атомарной точности литографиче-
ских процессов.
40 Введение в квантовые информационные технологии
Дальнейший прогресс в области вычислительных технологий, на наш
взгляд, будет связан с тем, что в дополнение к имеющимся технологиям при-
дут новые технологии, такие как оптические, молекулярные и квантовые
компьютеры. Наш нижеследующий рассказ посвящён описанию надежд,
которые исследователи в области квантовых информационных технологий
(КИТ) связывают с квантовыми компьютерами. В настоящее время кван-
товая информатика представляет собой новую быстро развивающуюся от-
расль науки, связанную с использованием квантовых систем для реализации
принципиально новых методов коммуникации и вычислений (квантовые ка-
налы связи, квантовая криптография, квантовый компьютер) [2, 83, 87–91].
Мы увидим, что некоторые основополагающие квантовые эффекты, которые
сейчас зачастую рассматриваются как помеха на пути технологий микро- и
наноэлектроники, могут оказаться источником радикальных новаций в об-
ласти вычислений.
1.3. Блеск и нищета современной физики
По оценке известного американского физика Джона Арчибальда Уилера
(1911–2008 гг.), примерно одна треть ВВП (валового внутреннего продукта)
Соединенных Штатов Америки непосредственно основана на достижениях
квантовой механики. Это и неудивительно, если учесть, что на этой науке
основана практически вся электроника, нанотехнологии, лазерные техноло-
гии, атомная промышленность, новые химические материалы и препараты
и т. п. Успешное развитие указанных отраслей невозможно без проведения
подробных расчётов квантовых систем, таких как наноструктуры, сложные
химические и биологические молекулы, новые лекарства и т. п. Однако, не-
смотря на впечатляющие успехи в изучении фундаментальных законов При-
роды, полномасштабное моделирование сложноорганизованных квантовых
систем всё ещё остаётся практически неосуществимой задачей.
Проиллюстрируем сказанное примером. Для полномасштабного моде-
лирования квантовых свойств атома железа нужно рассматривать движение
всех его 26 электронов в трёхмерном пространстве, что приводит к необхо-
димости решать уравнение Шрёдингера в конфигурационном пространстве
размерности 26 · 3 = 78 (и это без учёта спинов электронов, которые делают
динамику ещё более сложной). Если взять весьма грубую сетку, которая де-
лит каждую координату всего на 10 частей, то понадобится 1078 узлов для ре-
ализации соответствующей разностной схемы. Такого рода моделирование,
однако, никогда не сможет быть осуществлено хотя бы потому, что полное
число элементарных частиц во Вселенной, таких как протоны и нейтроны,
также «всего» порядка 1078. Таким образом, для моделирования всего одного
и далеко не самого сложного атома требуется ресурс, который превышает ме-
ханический ресурс всей Вселенной.
Глава 1. Квантовая механика и развитие информационных технологий 41
Мы видим, что квантовые задачи, за исключением простейших, явля-
ются алгоритмически очень сложными (практически неосуществимыми)
для вычислений на классическом компьютере. Из этого давно известного и,
на первый взгляд, негативного наблюдения Фейнман в 1982 г. сумел сделать
позитивный вывод: раз природа с успехом решает эти задачи, то, может быть,
и мы могли бы использовать квантовые системы в качестве некоторой новой
элементной базы для вычислений. Компьютеры, основанные на квантовых
логических элементах, могли бы быть намного более мощными по сравнению
со своими классическими собратьями. Интересно, что за два года до Фейн-
мана в 1980 г. похожие идеи выдвигал российский математик Юрий Манин
в своей небольшой, но очень содержательной книге «Вычислимое и невы-
числимое» [92].
1.4. Алгоритм Шора и некоторые другие
квантовые алгоритмы
Важным примером, на котором можно продемонстрировать радикальное
преимущество квантовых алгоритмов над классическими, является так назы-
ваемая задача факторизации, связанная с разложением целого числа на про-
стые множители. Оказывается, что в то время как умножение многозначных
чисел – это алгоритмически простая задача, обратная задача (разложение
на множители) алгоритмически очень сложна (обладает экспоненциальной
сложностью для всех известных в настоящее время классических алго-
ритмов).
Наилучший известный на сегодня классический алгоритм факторизации
целого числа (так называемый метод решета числового поля – general number
field sieve) требует для реализации следующее число операций:
exp((64 / 9)1/3 1/3(ln( ))2/3 ), class L n n (1.3)
где n = k log2 10 – число двоичных знаков, а k – число соответствующих деся-
тичных знаков, задающих это число.
Квантовый алгоритм факторизации, предложенный П. Шором в 1994 г.,
требует выполнения числа операций, выражаемым следующей формулой [41]:
2 ln( ) ln(ln( )). quant L n n n (1.4)
Сравнение формул (1.3) и (1.4) показывает, что алгоритм Шора пре-
вращает экспоненциально сложный алгоритм в алгоритм полиномиальной
сложности.
Мы взяли производительность компьютера экзафлопсного диапазона на
уровне 2 · 1018 оп/сек, что несколько превышает производительность двух са-
мых мощных на июнь 2024 года суперкомпьютеров: Frontier (Ок-Риджская
национальная лаборатория США) и Aurora (Аргоннская национальная ла-
42 Введение в квантовые информационные технологии
боратория США). Пересчёт от числа десятичных знаков k к числу двоичных
знаков n осуществлялся по формуле n = k log2 10.
Из таблицы 1.3 видно, что, например, самый мощный на сегодня супер-
компьютер экзафлопсного диапазона (2 · 1018 оп/сек) позволит разложить
число с k = 500 десятичными знаками за 600 миллиардов лет. Ту же задачу
квантовый компьютер мегагерцевого диапазона (1 млн квантовых операций
в секунду) решит за 41 секунду. Аналогично для числа с k = 1000 десятич-
ными знаками трудоёмкость классического алгоритма составляет 3 · 1024 лет,
а квантового – чуть более трёх минут.
Таким образом, квантовой компьютер, когда он будет создан, позволит
решать задачи, которые никогда не сможет решить классический компьютер.
В основе экспоненциального ускорения в алгоритме Шора лежит так
называемое квантовое преобразование Фурье. Для массива комплексных
амплитуд длины N число операций, необходимых для осуществления кван-
тового преобразования Фурье, есть величина порядка O((log N)2). Отметим,
что самые быстрые классические алгоритмы выполняют преобразование
Фурье за O(N(log N)) операций (так называемое быстрое преобразование
Фурье). Таким образом, квантовый алгоритм имеет экспоненциальное пре-
имущество по сравнению со своим классическим аналогом. Пусть, напри-
мер, имеется 1000-кубитовое состояние (n = 1000). Ему отвечает вектор
состояния, описывающийся N = 2n = 1,07 · 10301 комплексными числами.
Для осуществления классического быстрого преобразования потребуется
проделать порядка N log2 N = 1,07 · 10304 операций. В то же время квантовое
преобразование над рассматриваемым вектором осуществляется примерно
за (log2 N)2 = 1 · 106 операций.
Важно отметить следующее. Все известные на сегодня алгоритмы разло-
жения числа на простые множители на классическом компьютере являются
экспоненциально сложными. Если бы удалось доказать, что полиномиаль-
ного алгоритма в задаче факторизации чисел не существует вообще, то тем
самым удалось бы доказать абсолютное превосходство квантовых алгоритмов
над вероятностными классическими. Этот результат установил бы неравен-
ство классов сложности BPP и PSPACE, вопрос о взаимоотношении которых
является одной из ключевых открытых проблем современной теоретической
информатики.
Ещё один важный метод, иллюстрирующий квантовый параллелизм и
имеющий важное методическое значение, даёт алгоритм Дойча – Джозсы.
Суть этого результата заключается в следующем. Рассматривается функция
Таблица 1.3. Классический компьютер экзафлопсного диапазона (2 · 1018 оп/сек)
против квантового компьютера мегагерцевого диапазона (1 млн оп/сек)
Число десятичных знаков k k = 250 k = 500 k = 1000
Трудоёмкость классического алгоритма 140 лет 6 · 1011 лет 3 · 1024 лет
Трудоёмкость квантового алгоритма 9 сек 41 сек 190 сек
Глава 1. Квантовая механика и развитие информационных технологий 43
f (x) с n-битовой областью определения и 1-битовым множеством значений
(n – число кубитов). Переменная x может принимать n различных значе-
ний x = 0, 1, ..., N – 1, где N = 2n. Заранее известно, что функция f(x)может
быть только одного из двух типов: постоянная функция или так называе-
мая сбалансированная функция. Для постоянной функции f(0) = f (1) = ... =
= f(N – 1). Если функция сбалансирована, то f(x) = 0 для некоторых x и
f (x) = 1 для остальных значений аргумента, причём значения f(x) = 0 и
f (x) = 1 встречаются одинаково часто (в этом и заключается сбалансирован-
ность). Пусть, например, имеется функция f (x) с 10-битовой областью опре-
деления. Тогда для некоторых 512 значений x получим f (x) = 0, а для осталь-
ных 512 значений x получим f(x) = 1. Задача Дойча – Джозсы состоит в том,
чтобы отличить постоянную функцию от сбалансированной. Оказывается,
что алгоритм Дойча – Джозсы позволяет с достоверностью решить такую за-
дачу посредством одного-единственного обращения к вычислителю, кото-
рый определяется некоторым унитарным преобразованием Uf . В то же время
при классическом рассмотрении задачи Дойча – Джозсы для того, чтобы с до-
стоверностью отличить постоянную функцию от сбалансированной, может
потребоваться до 2n – 1 + 1 обращений к устройству, производящему вычисле-
ние функции f(x).
В качестве ещё одного замечательного результата стоит упомянуть ал-
горитм Гровера, который направлен на решение задач перебора, например
поиска записи в неструктурированной базе данных. Алгоритм Гровера обе-
спечивает поиск решения за O(√–
N) шагов в базе из N элементов. Заметим,
что классический алгоритм не способен решить задачу быстрее, чем за O(N)
шагов. Фактически при помощи алгоритма Гровера можно получать квадра-
тичное ускорение на NP-полных задачах.
Заметим, что алгоритм Гровера, как и квантовое преобразование
Фурье, смогут найти широкое применение в качестве важнейших состав-
ных частей при моделировании квантовых систем на квантовых компьюте-
рах. В то же время алгоритм факторизации Шора имеет большое значение
для задач криптографии. Создание полномасштабных квантовых компью-
теров и соответствующая реализация алгоритма Шора сделают беззащит-
ными системы классической криптографии с открытым ключом, такие как
RSA-код (назван по фамилиям авторов Р. Ривеста, А. Шамира и Л. Адлемана),
который сейчас используют для защиты информации в банковской
сфере и Интернете.
Таким образом, квантовые компьютеры, когда они будут созданы, позво-
лят решать задачи полномасштабного моделирования сложноорганизован-
ных квантовых систем, недоступные никаким классическим компьютерам,
а также некоторые другие важные задачи.
Важно отметить, что на пути создания квантового компьютера и кван-
товых алгоритмов встаёт множество задач, которые в силу экспоненциаль-
ного роста сложности относительно числа кубитов требуют больших вы-
44 Введение в квантовые информационные технологии
числительных ресурсов. Например, для анализа работы двадцатикубитового
квантового регистра требуется работа с матрицами размера 220×220. Работа
с такими матрицами трудна для современных персональных компьютеров,
однако может быть проделана при помощи суперкомпьютеров. Примеров
успешного применения высокопроизводительных вычислений в квантовой
информатике довольно много. Конечно же, добавление лишь нескольких де-
сятков кубитов поднимает данные задачи на уровень, недоступный никаким
суперкомпьютерам, но это как раз и означает, что использование наиболее
прогрессивных вычислительных технологий является критически важным
фактором для развития КИТ.
1.5. Кубит vs бит (логический анализ)
Основным элементом квантового компьютера является квантовый бит
(кубит), представляющий собой двухуровневую квантовую систему. В ка-
честве кубитов могут выступать ионы, атомы, электроны, фотоны, спины
атомных ядер, структуры из сверхпроводников и многие другие физические
системы. Проведём краткое сравнение кубита с физической реализаци-
ей классического бита информации на основе двоичного триггера с двумя
устойчивыми состояниями.
Так же как и классический бит, кубит может находиться в двух базисных
состояниях – |0〉 и |1〉. Пусть в качестве кубита выступает, например, атом.
Пусть, как показано на рисунке 1.2, |0〉 – это основное состояние, а |1〉 – не-
которое возбуждённое долгоживущее состояние. Именно эти состояния и
образуют кубит. Конечно, кроме указанных состояний у атома есть и мно-
го других состояний (одно из таких состояний, обозначенное как |2〉, пред-
ставлено на рисунке). Однако мы можем сделать так, что все другие воз-
буждённые состояния остаются практически невозмущёнными, если будем
управлять кубитом с помощью лазерного излучения, частота которого близка
к частоте перехода w01 между состояниями кубита |0〉 и |1〉 (только этот пере-
ход оказывается в резонансе с полем лазера, все остальные степени свободы
атома будут практически заморожены). Пусть вначале атом не возбуждён,
т. е. находится в состоянии |0〉. Перевод системы из состояния |0〉 в состоя-
ние |1〉 осуществляется с помощью так называемого p-импульса, который
задаётся посредством выбора длительности импульса лазерного излуче-
ния и напряжённости его электрического поля. Если же атом находится
в возбуждённом состоянии (на уровне |1〉) и на него ещё раз подействовать
p-импульсом, то атом перейдёт обратно в состояние |0〉. Такое поведение пол-
ностью аналогично поведению классического бита и, если бы всё ограничива-
лось этим, то не было бы никакой разницы между классической и квантовой
информацией.
Однако давайте теперь рассмотрим, что произойдёт, если подействовать
на атом не p-импульсом, а импульсом вдвое меньшей длительности, т. е. им-
Глава 1. Квантовая механика и развитие информационных технологий 45
пульсом p/2. В этом случае атом начнёт свой переход из состояния |0〉 в со-
стояние |1〉, но не успеет завершить его. В результате, как оказывается, воз-
никнет состояние квантовой статистической неопределённости, которое мы
можем условно записать как состояние суперпозиции (|0〉 + |1〉)/√–
2. В этой
записи нет ничего таинственного. Она означает, что кубит может с вероятно-
стью 1/2 оказаться в состоянии |0〉 и с такой же вероятностью 1/2 – в состоя-
нии |1〉 (см. ниже). Здесь 1/√–
2 – амплитуда вероятности, а вероятность, в со-
ответствии с законами квантовой механики, есть квадрат модуля амплитуды.
Такое поведение кубита обусловлено его фундаментальной информационной
ограниченностью (между показанными на рисунке уровнями |0〉 и |1〉 про-
сто нет никаких «полочек», на которых атом мог бы «остановиться» по пути
от одного состояния к другому).
Как хорошо известно, поведение классического бита информации со-
всем другое. Например, в микросхемах на основе транзисторно-транзи-
сторной логики (ТТЛ) логический ноль представляется определённым низ-
ким напряжением в диапазоне от нуля до 0,8 В, в то время как логическая
единица – определённым уровнем высокого напряжения в диапазоне от 2,4
до 5,0 В. При этом, конечно, в системе физически возможны и любые другие
промежуточные значения напряжения между логическими нулём и едини-
цей, которые фактически отвечают неисправности схемы. В отличие от кван-
тового бита, классический бит представляет собой физическую систему
с практически неограниченным числом степеней свободы и состояний, сре-
ди которых условно выбираются «ноль» и «единица». Таким образом, самое
главное (и фундаментальное) отличие кубита от классического бита состоит
в том, что в основе первого лежит естественное квантование информации,
в то время как в основе второго – искусственная дискретизация аналогового
сигнала.
Информационная ограниченность квантовых систем приводит к необ-
ходимости их статистического описания. Согласно квантовой механике, со-
стояние физической системы задаётся с помощью таких объектов, как вол-
новая функция и матрица плотности, которые, образно говоря, составляют
«полный каталог знаний», позволяющий правильно рассчитать вероятности
Рис. 1.2. Квантовый бит (кубит) на примере энергетических уровней атомов
46 Введение в квантовые информационные технологии
исходов любых будущих измерений. Важно отметить, что статистическая
неопределённость квантовых систем, в отличие от классических, является
управляемой. Так, упомянутое выше состояние (|0〉 + |1〉)/√–
2 не несёт в себе
никакой энтропийной неопределённости. Энтропия этого состояния оказы-
вается равной нулю, поскольку посредством преобразования p/2 (либо, что
то же самое, 3p/2) оно может быть обратно приведено в состояние «ноль».
Такое управление было бы невозможно, если бы мы имели просто класси-
ческую ситуацию, когда половина представителей ансамбля находятся в со-
стоянии «ноль», а половина – в состоянии «единица». В классическом слу-
чае вероятность является субъективной, поскольку исследователь просто
«не знает» «истинного» состояния дел.
Заметим, что безэнтропийными являются все так называемые чистые со-
стояния. Любое такое состояние можно посредством вполне определённого
обратимого унитарного преобразования привести в состояние «ноль». Любое
чистое состояние может быть задано посредством вектора состояния (волно-
вой функции) в гильбертовом пространстве. Представленные выше обозна-
чения, введённые Дираком, такие как |0〉, |1〉, (|0〉 + |1〉)/√–
2 и т. п., как раз дают
примеры векторов квантовых состояний. При этом состояния логического
нуля и единицы оказываются ортогональными друг другу: 〈0|1〉 = 0. Фунда-
ментальное правило, открытое Борном и фон Нейманом и определяющее
статистический аспект квантовой теории, гласит, что вероятность обнару-
жить систему в состоянии |j〉 при условии, что она была приготовлена в со-
стоянии |y〉, задаётся квадратом модуля их скалярного произведения:
F = | 〈j|y〉 |2. (1.5)
Введённая величина F называется степенью согласованности или ве-
роятностью совпадения квантовых состояний fidelity. Если, например,
|y〉 = (|0〉 + |1〉)/√–
2 , а |j〉 = |0〉, то 〈j|y〉 = 1/√–
2 и F = 1/2.
Заметим, что наряду с чистыми состояниями существуют и так называ-
емые смешанные состояния, описываемые в рамках формализма матрицы
плотности и соответствующие некогерентным смесям чистых состояний
(см. раздел 2.3). Смешанные состояния обладают энтропией, которую можно
вычислить по формуле фон Неймана:
2 log . j j
j
S (1.6)
Эта формула является квантовым аналогом известной формулы Шенно-
на (причём, в роли вероятностей выступают собственные значения матри-
цы плотности lj). Заметим, однако, что исторически формула фон Нейма-
на возникла раньше, в 1932 г., в то время как Шеннон ввёл свою энтропию
только в 1948 г. Более того, по свидетельству Шеннона, сама идея исполь-
зовать термин «энтропия» была подсказана ему фон Нейманом в частной
беседе.
Глава 1. Квантовая механика и развитие информационных технологий 47
Смешанные состояния несут в себе ненулевую энтропию, обусловлен-
ную информационной связью квантовой системы с её окружением. Эта связь
приводит к своеобразному «уходу» информации из системы в окружение,
в результате теряется квантовая когерентность системы и возможность авто-
номного управления её состоянием. Фактически вместо состояния собствен-
но исходной квантовой системы возникает единое состояние более крупного
объекта «система + окружение» (этим состоянием, однако, зачастую трудно
или даже невозможно управлять практически).
1.6. Представление состояния кубита
на сфере Блоха
Квантовое состояние кубита представляет собой суперпозицию двух базис-
ных состояний физической системы:
0
0 1 0 1
1
1 ,
1 0
0
0 1
c
c c c c
c
(1.7)
где условие |c0|2 + |c1|2 = 1 задаёт нормировку на единицу полной вероятности
состояния кубита.
Рис. 1.3. Кубит на сфере Блоха
Оказывается, что всё множество квантовых состояний кубита можно на-
глядно представить на так называемой сфере Блоха, очень похожей на гло-
бус. Каждое чистое однокубитовое состояние задаётся точкой на сфере Бло-
ха, положение которой определяется полярным q и азимутальным j углами
(рис. 1.3):
48 Введение в квантовые информационные технологии
cos exp
2 2
sin exp
2 2
i
i
. (1.8)
Кубит «живёт» одновременно в абстрактном двумерном гильбертовом
пространстве и в обычном трёхмерном евклидовом пространстве. Вычисли-
тельные операции задаются посредством унитарных вращений на сфере Бло-
ха. Оператор унитарных вращений на угол q относительно единичной оси n→
определяется следующей формулой:
( ) exp( ) cos sin ,
2 2 2 nR i n I i n
(1.9)
где s→ = (s1, s2, s3) – матрицы Паули, I – единичная матрица.
Параметры вращения на сфере Блоха (направление оси вращения и вели-
чина угла поворота) задаются теми физическими воздействиями, которые мы
оказываем на квантовый объект (напряжённостями полей, частотами, поля-
ризациями, длительностью воздействий и т. п.). Аналогичное утверждение
справедливо не только для отдельного кубита, но и для регистра из n кубитов
(только теперь гильбертово пространство имеет размерность 2n).
Таким образом, каждой точке сферы Блоха соответствует некоторое со-
стояние кубита и каждому состоянию кубита – некоторая точка на сфере
Блоха. Например, состояние |0〉 соответствует северному полюсу, а состоя-
ние |1〉 – южному полюсу. При воздействии p/2-импульса на невозмущённый
атом кубит движется от северного полюса до экватора вдоль некоторого ме-
ридиана (например, на рис. 1.3 происходит вращение вокруг оси y).
Заметим, что если бы мы взяли импульс не p/2, а ещё вдвое короче,
т. е. p/4, то кубит в процессе своей эволюции остановился бы не на экваторе,
а на широте 45 градусов в северном полушарии, а если бы мы взяли импульс
3p/4, то оказались бы уже в южном полушарии на широте 45 градусов, и т. д.
Вообще всегда можно подобрать некоторое воздействие на кубит, которое
переведёт его из одной произвольно заданной точки на сфере Блоха в любую
другую, наперёд заданную. Все преобразования такого рода принято называть
унитарными вращениями. С помощью таких вращений можно осуществлять
«навигацию» кубита на сфере Блоха (например, мы можем направить его
из точки с координатами Москвы в точку с координатами Рио-де-Жанейро).
Но следует помнить, что эта красивая картинка – только визуализация
неопределённости квантового состояния. Как бы ни двигался кубит по гло-
бусу, придуманному Блохом, при стандартном измерении он всё равно в кон-
це концов окажется либо на северном полюсе, либо на южном. Чем ближе
кубит к северному полюсу, тем вероятнее, что при измерении он будет об-
наружен в состоянии |0〉, а чем ближе он к южному полюсу, тем вероятнее,
Глава 1. Квантовая механика и развитие информационных технологий 49
что он будет обнаружен в состоянии |1〉. В результате измерения происходит
так называемый квантовый скачок. И где бы ни находился кубит, в результате
квантового скачка он всегда оказывается на полюсе (северном или южном).
1.7. Квантовое измерение и квантовый
скачок
Измерение является весьма сильным стрессовым воздействием на квантовую
систему. Рассмотрим эту операцию на примере типичных измерений в ато-
мах. Вспомним, что наряду с кубитовыми состояниями |0〉 и |1〉 у атома име-
ется и много других состояний. Рассмотрим одно из них, которое на рис. 1.2
обозначено как |2〉. Удобно в качестве уровня |2〉 выбрать такой, который,
в отличие от уровня |1〉, является не долгоживущим, а короткоживущим.
Это означает, что атом, оказавшись на этом уровне, долго там не задержи-
вается, а весьма быстро перескакивает в основное состояние |0〉 (при таком
перескоке, конечно, излучается фотон, который уносит имевшуюся у атома
энергию возбуждения). До сих пор существование этого состояния не имело
для нас решительно никакого значения, поскольку лазерное поле, которое
мы использовали, было резонансным только по отношению к переходу меж-
ду состояниями |0〉 и |1〉, а все другие состояния атома для этого поля практи-
чески не существовали. Но теперь давайте сделаем активным переход между
уровнями |0〉 и |2〉. Для этого используем лазерное излучение соответству-
ющей частоты, близкой к частоте w02 этого перехода. Теперь атом получает
возможность активно эволюционировать между состояниями |0〉 и |2〉. Если
уровень |0〉 окажется заселён, то новое лазерное поле неизбежно приведёт
к заселению и уровня |2〉, но поскольку время жизни на этом уровне мало,
атом быстро излучит фотон в случайном направлении в пространстве и снова
скатится на уровень |0〉, откуда под действием того же лазерного поля снова
поднимется вверх, снова излучит фотон и снова скатится вниз (и так много
раз подряд, в результате получится, что атом «засветится» – это явление на-
зывается лазерной флуоресценцией).
А теперь давайте вспомним, что до измерения атом находился ни в со-
стоянии |0〉, ни в состоянии |1〉, а в некотором состоянии квантовой стати-
стической неопределённости (суперпозиции), которое мы описали ранее.
Теперь, после того как мы сделали активным переход между состояниями |0〉
и |2〉, атом не может больше находиться в состоянии «задумчивости», он вы-
нужден сделать выбор между двумя несовместимыми альтернативами: либо
свалиться в состояние |0〉 и начать активно флуоресцировать, либо «спрятать-
ся» от внешнего лазерного воздействия в состоянии |1〉, которое нечувстви-
тельно к прилагаемому лазерному полю. В результате кубит, находящийся
в произвольной точке сферы Блоха, вынужденно совершит квантовый ска-
чок и окажется либо на северном полюсе (в состоянии |0〉), либо на южном
50 Введение в квантовые информационные технологии
полюсе в состоянии |1〉. При этом если кубит осуществлял свою «навигацию»
в северном полушарии, то, скорее всего, с вероятностью более 50% в соответ-
ствии с формулой (1.5) в результате квантового скачка он окажется на север-
ном полюсе, а если он был в южном полушарии, то, скорее всего, окажется
на южном полюсе (конечно, не исключено, что кубит из широт северного
полушария окажется на южном полюсе и, наоборот, кубит из широт южного
полушария окажется на северном полюсе, но вероятность такого рода про-
цессов заведомо ниже 50%).
Таким образом, имеет место своеобразный «закон инерции квантовой
информации», согласно которому «всякая квантовая система продолжает
удерживаться в своём состоянии квантовой статистической неопределённо-
сти, пока и поскольку информационное воздействие со стороны окружения
не понуждает её сделать выбор между различными альтернативами в пользу
какой-то одной». В нашем примере, пока переход между состояниями |0〉 и |2〉
не был освещён, атому не было никакой нужды выбирать между |0〉 и |1〉, по-
этому он мог бы находиться очень долго в состоянии «задумчивости» и «не-
решительности»: что выбрать – |0〉 или |1〉? Но как только переход |0〉 → |2〉
был освещён ярким светом, ему пришлось выбирать: либо быть в нуле,
тогда нужно светиться, флуоресцировать, либо же «прятаться» на «тём-
ной» энергетической полке |1〉, нечувствительной к лазерному излучению
с частотой w02.
1.8. Системы кубитов и квантовая
запутанность
Однокубитовое состояние (1.7) имеет в своей основе два базисных состояния
(|0〉 и |1〉). У системы из двух кубитов таких базисных состояний уже четыре:
|00〉, |01〉, |10〉, |11〉. Запись |01〉, например, означает, что первый кубит находит-
ся в состоянии «ноль», а второй – в состоянии «единица» и т. д.
Система из двух кубитов может находиться не только в каждом из четы-
рех базисных состояний, но и в состояниях, представляющих собой суперпо-
зиции базисных:
|y〉 = c00|00〉 + c01|01〉 + c10|10〉 + c11|11〉. (1.10)
Неожиданным с точки зрения обычной интуиции является то, что состо-
яние системы не всегда описывается в терминах состояния отдельных её ча-
стей. Например, такое состояние из двух кубитов, как (|00〉 + |11〉)/√–
2, не мо-
жет быть разложено отдельно на состояния каждого из двух кубитов. Другими
словами, мы не можем найти такие комплексные числа a1, b1, a2, b2, которые
обеспечивали бы выполнение следующего равенства:
(a1 |0〉 + b1 |1〉) ⊗ (a2 |0〉 + b2 |1〉) = |00〉 + |11〉. (1.11)
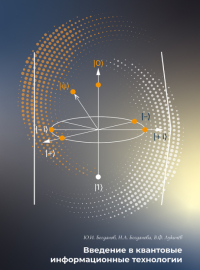
 eng
eng

